题目内容
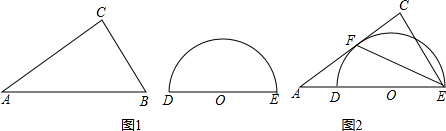
10.如图1,水平放置一个三角板和一个量角器,三角板的边AB和量角器的直径DE在一条直线上,∠ACB=90°,∠BAC=30°,OD=3cm,开始的时候BD=1cm,现在三角板以2cm/s的速度向右移动.(1)当点B于点O重合的时候,求三角板运动的时间;
(2)三角板继续向右运动,当B点和E点重合时,AC与半圆相切于点F,连接EF,如图2所示.
①求证:EF平分∠AEC;
②求EF的长.
分析 (1)由当点B于点O重合的时候,BO=OD+BD=4cm,又由三角板以2cm/s的速度向右移动,即可求得三角板运动的时间;
(2)①连接OF,由AC与半圆相切于点F,易得OF⊥AC,然后由∠ACB=90°,易得OF∥CE,继而证得EF平分∠AEC;
②由△AFO是直角三角形,∠BAC=30°,OF=OD=3cm,可求得AF的长,由EF平分∠AEC,易证得△AFE是等腰三角形,且AF=EF,则可求得答案.
解答 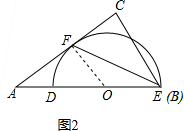 解:(1)∵当点B于点O重合的时候,BO=OD+BD=4cm,
解:(1)∵当点B于点O重合的时候,BO=OD+BD=4cm,
∴t=$\frac{4}{2}$=2(s);
∴三角板运动的时间为:2s;
(2)①证明:连接O与切点F,则OF⊥AC,
∵∠ACE=90°,
∴EC⊥AC,
∴OF∥CE,
∴∠OFE=∠CEF,
∵OF=OE,
∴∠OFE=∠OEF,
∴∠OEF=∠CEF,
即EF平分∠AEC;
②解:由①知:OF⊥AC,
∴△AFO是直角三角形,
∵∠BAC=30°,OF=OD=3cm,
∴tan30°=$\frac{3}{AF}$,
∴AF=3$\sqrt{3}$cm,
由①知:EF平分∠AEC,
∴∠AEF=∠CEF=$\frac{1}{2}$∠AEC=30°,
∴∠AEF=∠EAF,
∴△AFE是等腰三角形,且AF=EF,
∴EF=3$\sqrt{3}$cm.
点评 此题属于圆的综合题.考查了切线的性质、等腰三角形的判定与性质以及三角函数等知识.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
20.抛物线y=2(x+3)(x-1)的对称轴是( )
| A. | x=1 | B. | x=-1 | C. | x=$\frac{1}{2}$ | D. | x=-2 |
2.下列命题中,是真命题的是( )
| A. | 平分弦的直径垂直于弦 | B. | 相等圆周角所对的弧相等 | ||
| C. | 任意三个点确定一个圆 | D. | 圆内接平行四边形必为矩形 |
19.2015年,菏泽市相关部门统计,春节一周长假期间共实现销售收入约3.284亿元,比同期增长4.8%,请你将3.284亿用科学记数法表示为( )
| A. | 3.284×108 | B. | 32.84×107 | C. | 3.284×107 | D. | 32.84×108 |
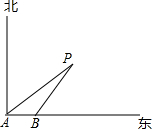 如图,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,求轮船与灯塔的最短距离.(精确到0.1,$\sqrt{3}$≈1.73)
如图,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,求轮船与灯塔的最短距离.(精确到0.1,$\sqrt{3}$≈1.73)