题目内容
11.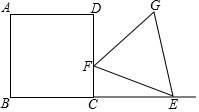 如图,正方形ABCD的边长为3,点E在线段BC的延长线上,且CE=CD,点F是直线CD上的动点,以EF为边作正三角形EFG,若GE⊥BE,则DF=3-$\sqrt{3}$或3+$\sqrt{3}$.
如图,正方形ABCD的边长为3,点E在线段BC的延长线上,且CE=CD,点F是直线CD上的动点,以EF为边作正三角形EFG,若GE⊥BE,则DF=3-$\sqrt{3}$或3+$\sqrt{3}$.
分析 根据题意可以得到∠FEC的度数,然后根据题目中的条件和锐角三角函数,可以求得DF的长.
解答 解:∵正方形ABCD的边长为3,点E在线段BC的延长线上,且CE=CD,
∴BE=6,CE=CD=3,
∵△EFG是等边三角形,GE⊥BE,
∴∠FEC=30°,
∴tan∠FEC=$\frac{CF}{CE}$,
即$\frac{\sqrt{3}}{3}=\frac{CF}{3}$,
∴CF=$\sqrt{3}$,
∵CD=3,
∴DF=CD-CF=3-$\sqrt{3}$或DF=CD+CF=3+$\sqrt{3}$,
故答案为:3$-\sqrt{3}$或3+$\sqrt{3}$.
点评 本题考查正方形的性质、等边三角形的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用锐角三角函数解答.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
 如图,已知∠A=∠E,AB∥EC,求证:AC∥ED.
如图,已知∠A=∠E,AB∥EC,求证:AC∥ED.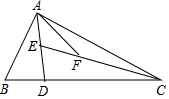 如图,BC=5BD,E是AD的中点,F是EC的三等分点,已知△AEF的面积是4平方厘米,则△ABD的面积多少平方厘米?
如图,BC=5BD,E是AD的中点,F是EC的三等分点,已知△AEF的面积是4平方厘米,则△ABD的面积多少平方厘米?