题目内容
8.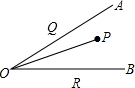 如图,∠AOB=45°,∠AOB内有一定点P,且OP=10.在OA上有一动点Q,OB上有一动点R.若△PQR周长最小,则最小周长是( )
如图,∠AOB=45°,∠AOB内有一定点P,且OP=10.在OA上有一动点Q,OB上有一动点R.若△PQR周长最小,则最小周长是( )| A. | 10 | B. | 10$\sqrt{2}$ | C. | 20 | D. | 20$\sqrt{2}$ |
分析 作点P关于OA的对称点P1,关于OB的对称点P2,连接P1P2与OA、OB分别相交于点Q、R,根据轴对称的性质可得PQ=P1Q,PR=P2R,从而得到△PQR的周长=P1P2并且此时有最小值,连接P1O、P2O,再求出△P1OP2为等腰直角三角形,再根据等腰直角三角形的性质求解即可.
解答  解:如图,作点P关于OA的对称点P1,关于OB的对称点P2,连接P1P2与OA、OB分别相交于点Q、R,
解:如图,作点P关于OA的对称点P1,关于OB的对称点P2,连接P1P2与OA、OB分别相交于点Q、R,
所以,PQ=P1Q,PR=P2R,
所以,△PQR的周长=PQ+QR+PR=P1Q+QR+P2R=P1P2,
由两点之间线段最短得,此时△PQR周长最小,
连接P1O、P2O,则∠AOP=∠AOP1,OP1=OP,∠BOP=∠BOP2,OP2=OP,
所以,OP1=OP2=OP=10,∠P1OP2=2∠AOB=2×45°=90°,
所以,△P1OP2为等腰直角三角,
所以,P1P2=$\sqrt{2}$OP1=10$\sqrt{2}$,
即△PQR最小周长是10$\sqrt{2}$.
故选B.
点评 本题考查了轴对称确定最短路线问题,轴对称的性质,等腰直角三角形的判定与性质,难点在于作辅助线得到与△PQR周长相等的线段.

练习册系列答案
相关题目
19.抛物线y=-3x2+12x-7的顶点坐标为( )
| A. | (2,5) | B. | (2,-19) | C. | (-2,5) | D. | (-2,-43) |
16.二次函数y=-2x2+4x+5的对称轴为( )
| A. | x=2 | B. | 直线x=2 | C. | x=1 | D. | 直线x=1 |
17.若3am-2b3与$\frac{1}{2}$abn+1是同类项,则m+n=( )
| A. | _3 | B. | 3 | C. | 5 | D. | -5 |
18.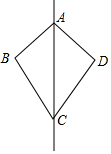 如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为( )
如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为( )
 如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为( )
如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为( )| A. | 55° | B. | 65° | C. | 75° | D. | 85° |
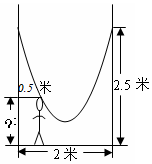 如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,最低点离地面0.5米,小明距较近的那棵树0.5米时,头部刚好接触到绳子,则小明的身高为1米.
如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,最低点离地面0.5米,小明距较近的那棵树0.5米时,头部刚好接触到绳子,则小明的身高为1米. 已知△ABC,用直尺和圆规作下列图形:(保留作图痕迹并写出结论)
已知△ABC,用直尺和圆规作下列图形:(保留作图痕迹并写出结论) 如图,△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,EF交BC于F,交AB于E,BF=5cm,求CF的长.
如图,△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,EF交BC于F,交AB于E,BF=5cm,求CF的长.