题目内容
9.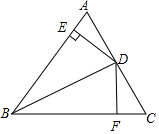 如图,BD是∠ABC的平分线,DE⊥AB,DF⊥BC,垂足分别为E、F,若△ABC的面积为36cm2,AB=18cm,BC=12cm,求DE的长.
如图,BD是∠ABC的平分线,DE⊥AB,DF⊥BC,垂足分别为E、F,若△ABC的面积为36cm2,AB=18cm,BC=12cm,求DE的长.
分析 先根据角平分线的性质得出DE=DF,再由三角形的面积公式即可得出结论.
解答 解:∵如图,BD是∠ABC的平分线,DE⊥AB,垂足为点E,DF⊥BC,垂足为F,
∴DE=DF.
∵S△ABC=30,AB=18,BC=12,
∴S△ABD+S△BCD=$\frac{1}{2}$AB•DE+$\frac{1}{2}$BC•DF=36,即$\frac{1}{2}$×18DE+$\frac{1}{2}$×12DE=36,
解得DE=$\frac{12}{5}$.
点评 本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
相关题目
4.下列条件中,不能判定△ABC≌△A'B'C'的是( )
| A. | ∠A=∠A',∠C=∠C',AC=A'C' | |
| B. | ∠B=∠B',BC=B'C',AB=A'B' | |
| C. | ∠A=∠A'=80°,∠B=60°,∠C'=40°,AB=A'B' | |
| D. | ∠A=∠A',BC=B'C',AB=A'B' |
14.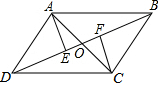 如图,已知AB∥CD,AD∥BC,AC与BD交于点O,AE⊥BD于点E,CF⊥BD于点F,那么图中全等的三角形有( )
如图,已知AB∥CD,AD∥BC,AC与BD交于点O,AE⊥BD于点E,CF⊥BD于点F,那么图中全等的三角形有( )
 如图,已知AB∥CD,AD∥BC,AC与BD交于点O,AE⊥BD于点E,CF⊥BD于点F,那么图中全等的三角形有( )
如图,已知AB∥CD,AD∥BC,AC与BD交于点O,AE⊥BD于点E,CF⊥BD于点F,那么图中全等的三角形有( )| A. | 5对 | B. | 6对 | C. | 7对 | D. | 8对 |
19.如果一个单项式与-3ab的积为-$\frac{3}{4}$a2bc,则这个单项式为( )
| A. | $\frac{1}{4}$ a2c | B. | $\frac{1}{4}$ ac | C. | $\frac{9}{4}$ a2c | D. | $\frac{9}{4}$ ac |
 如图,已知△ABF≌△DCE,BE、FC在同一直线上,BE=2cm,求CF的长.
如图,已知△ABF≌△DCE,BE、FC在同一直线上,BE=2cm,求CF的长.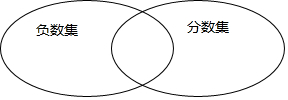 如图,两个圈分别表示负数集和分数集,请将3,0,$\frac{1}{2}$,-3$\frac{1}{3}$,-5,-3.4中符合条件的数填入圈中.
如图,两个圈分别表示负数集和分数集,请将3,0,$\frac{1}{2}$,-3$\frac{1}{3}$,-5,-3.4中符合条件的数填入圈中.