如图.在△ABC中.AB=AC.以AB为直径的⊙O交BC于点D.过点D作EF⊥AC于点E.交AB的延长线于点F．(1)判断直线DE与⊙O的位置关系.并说明理由,(2)如果AB=5.BC=6.求DE的长． DE=． [解析]试题分析:(1)连接AD.OD.根据已知条件证得OD⊥DE即可, (2)根据勾股定理计算即可． [解析] (1)相切. 理由如下: 题目和参考答案——青夏教育精英家教网——

题目内容

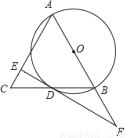
如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作EF⊥AC于点E，交AB的延长线于点F．

（1）判断直线DE与⊙O的位置关系，并说明理由；

（2）如果AB=5，BC=6，求DE的长．

（1）相切，理由见解析；（2）DE=．【解析】试题分析：（1）连接AD，OD，根据已知条件证得OD⊥DE即可；（2）根据勾股定理计算即可．【解析】（1）相切，理由如下：连接AD，OD， ∵AB为⊙O的直径， ∴∠ADB=90°． ∴AD⊥BC． ∵AB=AC， ∴CD=BD=BC． ∵OA=OB， ∴OD∥AC．...

练习册系列答案

培优新航标系列答案

培优大视野系列答案

仁爱地理同步练习册系列答案

牛津英语活动练习手册系列答案

牛津英语基础训练系列答案

牛津英语随堂讲与练系列答案

牛津英语一课一练系列答案

中考真题及模拟试题汇编系列答案

中考复习指南针江苏系列答案

魔力导学开心练系列答案

相关题目

如图，已知，AB∥CD，直线EF分别交AB，CD于E、F，点G在直线EF上，GH⊥AB，若∠EGH=32°，则∠DFE的度数为____________.

58° 【解析】【解析】 ∵GH⊥AB，∴∠GHE=90°，∵∠G+∠GHE+∠GEH=180°，∠EGH=32°，∴∠GEH=58°，∵AB∥CD，∴∠DFE=∠GEH=58°．故答案为：58°．

一个多边形的内角和是它的外角和的2倍，则这个多边形是( )

A. 四边形 B. 五边形 C. 六边形 D. 七边形

C 【解析】【解析】设多边形边数为n，根据题意，得：（n﹣2）•180=720，解得：n=6，故选C．

某中学课外兴趣活动小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边由长为30米的篱笆围成．已知墙长为18米（如图所示），设这个苗圃园垂直于墙的一边长为x米．

（1）若苗圃园的面积为72平方米，求x；

（2）若平行于墙的一边长不小于8米，这个苗圃园的面积有最大值和最小值吗？如果有，求出最大值和最小值；如果没有，请说明理由．

（1）12（2）当x=11时，y最小=88平方米【解析】（1）根据题意得方程解即可；（2）设苗圃园的面积为y，根据题意得到二次函数的解析式y=x（30-2x）=-2x2+30x，根据二次函数的性质求解即可. 【解析】 (1)苗圃园与墙平行的一边长为(30－2x)米．依题意可列方程 x(30－2x)＝72，即x2－15x＋36＝0．解得x1＝3（舍去），x2＝1...

某商品现在的售价为每件60元，每星期可卖出300件．市场调查反映，如果调整商品售价，每降价1元，每星期可多卖出20件．设每件商品降价x元后，每星期售出商品的总销售额为y元，则y与x的关系式为（　　）

A. y=60（300+20x） B. y=（60﹣x）（300+20x）

C. y=300（60﹣20x） D. y=（60﹣x）（300﹣20x）

B 【解析】每件商品降价x元后，则每星期的销售量为(300＋20x)件，单价为(60－x)元，则y＝(60－x)(300＋20x)，故选B.

如图，在边长均为l的小正方形网格纸中，△ABC的顶点，A、B、C均在格点上，O为直角坐标系的原点，点A（-1，0）在x轴上．

（1）以O为位似中心，将△ABC放大，使得放大后的△A1B1C1与△ABC的相似比为2：1，要求所画△A1B1C1与△ABC在原点两侧；

（2）分别写出B1、C1的坐标．

（1）画图见解析；（2）B1、C1的坐标分别为：（4，-4），（6，-2）．【解析】试题分析：（1）连接OA并延长，使OA1=2OA，同法得到其余各点，顺次连接即可；（2）根据所得图形及网格图即可得出答案．【解析】（1）所画图形如下所示： △A1B1C1即为所求. （2）B1、C1的坐标分别为：（4，-4），（6，-2）．

已知CD是Rt△ABC斜边上的高线，且AB=10，若BC=8，则cos∠ACD= ______ ．

【解析】试题分析：根据同角的余角相等得：∠ACD=∠B，利用同角的余弦得结论．【解析】 ∵CD是Rt△ABC斜边上的高线， ∴CD⊥AB， ∴∠A+∠ACD=90°， ∵∠ACB=90°， ∴∠B+∠A=90°， ∴∠ACD=∠B， ∴cos∠ACD=cos∠B===，故答案为： .

七、八年级学生分别到雷锋、毛泽东纪念馆参观，共589人，到毛泽东纪念馆的人数是到雷锋纪念馆人数的2倍多56人．设到雷锋纪念馆的人数为x人，可列方程为_______________．

2x＋56＝589－x 【解析】试题分析：因为设到雷锋纪念馆的人数为人，所以到毛泽东纪念馆的人数是（2x+56）人，根据共人，可列方程得：．

如图，将等边△ABC绕点C顺时针旋转120°得到△EDC，连接AD，BD．则下列结论：

①AC=AD；②BD⊥AC；③四边形ACED是菱形．

其中正确的个数是（）

A．0 B．1 C．2 D．3

D．【解析】试题分析：根据旋转和等边三角形的性质得出∠ACE=120°，∠DCE=∠BCA=60°，AC=CD=DE=CE，求出△ACD是等边三角形，求出AD=AC，根据菱形的判定得出四边形ABCD和ACED都是菱形，根据菱形的判定推出AC⊥BD． ∵将等边△ABC绕点C顺时针旋转120°得到△EDC， ∴∠ACE=120°，∠DCE=∠BCA=60°，AC=CD=DE=CE， ∴∠ACD...