题目内容
20.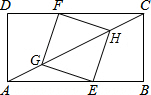 如图,在矩形ABCD 中,AB=8,BC=4,点E在AB上,点F在CD上,点G、H在对角线AC上,若四边形EGFH是正方形,则△AGE的面积为$\frac{5}{2}$.
如图,在矩形ABCD 中,AB=8,BC=4,点E在AB上,点F在CD上,点G、H在对角线AC上,若四边形EGFH是正方形,则△AGE的面积为$\frac{5}{2}$.
分析 先根据正方形的性质和矩形的性质,判定△CFO≌△AOE,并求得AO的长,再判定△AOE∽△ABC,求得OE和AG的长,最后计算△AGE的面积.
解答 解:连接EF交AC于O,
∵四边形EGFH是正方形,
∴EF⊥AC,OE=OF,
∵四边形ABCD是矩形,
∴∠B=∠D=90°,AB∥CD,
∴∠ACD=∠CAB,
在△CFO与△AOE中, $\left\{\begin{array}{l}{∠FCO=∠OAB}\\{∠FOC=∠AOE}\\{OF=OE}\end{array}\right.$,
$\left\{\begin{array}{l}{∠FCO=∠OAB}\\{∠FOC=∠AOE}\\{OF=OE}\end{array}\right.$,
∴△CFO≌△AOE(AAS),
∴AO=CO,
∵AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=4$\sqrt{5}$,
∴AO=$\frac{1}{2}$AC=2$\sqrt{5}$,
∵∠CAB=∠EAO,∠AOE=∠B=90°,
∴△AOE∽△ABC,
∴$\frac{OE}{BC}=\frac{AO}{AB}$,即$\frac{OE}{4}=\frac{2\sqrt{5}}{8}$
∴OE=$\sqrt{5}$=OG
∴AG=AO-GO=2$\sqrt{5}$-$\sqrt{5}$=$\sqrt{5}$
∵EF⊥AC
∴△AGE的面积=$\frac{1}{2}$×AG×OE=$\frac{1}{2}$×$\sqrt{5}$×$\sqrt{5}$=$\frac{5}{2}$
故答案为:$\frac{5}{2}$
点评 本题主要考查了正方形的性质,解决问题的关键是掌握全等三角形的判定与性质,以及相似三角形的判定与性质.本题若不运用相似三角形,则可以过点F作AB的垂线,构造直角三角形,并运用勾股定理进行计算求解.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
11. 如图,在?ABCD中,对角线AC、BD相交于点O,点E、F分别是AD、CD的中点,则△OEF的面积S1与△BOC面积S2的关系是( )
如图,在?ABCD中,对角线AC、BD相交于点O,点E、F分别是AD、CD的中点,则△OEF的面积S1与△BOC面积S2的关系是( )
 如图,在?ABCD中,对角线AC、BD相交于点O,点E、F分别是AD、CD的中点,则△OEF的面积S1与△BOC面积S2的关系是( )
如图,在?ABCD中,对角线AC、BD相交于点O,点E、F分别是AD、CD的中点,则△OEF的面积S1与△BOC面积S2的关系是( )| A. | S1=S2 | B. | S1>S2 | C. | S1<S2 | D. | $S1=\frac{1}{2}S2$ |
8.国家发改委决定,自2015年6月1日起全面放开药品价格,在市场机制作用下,今年春节后3月1日起,部分常用抗生素药品零售价出现下降,合肥某药房对售出的涉及降价的抗生素药品中A、B、C、D药的售价变化及今年2月份抗生素销量情况进行了统计,并绘制成如下统计图:
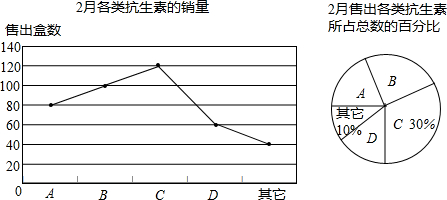
(1)2月份该药房共售出抗生素400盒;若3月份各种抗生素的销量按2月份的销量计算,则3月份A、B、C、D四种抗生素的销售额比2月份减少了904元;
(2)补全扇形统计图;
(3)吴老师到该药房买一些抗生素作为家里备用药,在A、B、C、D各一盒中随机购买两盒,请用画树状图或列表法求出他刚好选中A和B的概率.

| A | B | C | D | |
| 2月份售价(元/盒) | 15.4 | 8.6 | 11.2 | 28.2 |
| 3月份售价(元/盒) | 12.8 | 7.7 | 10 | 20.5 |
(2)补全扇形统计图;
(3)吴老师到该药房买一些抗生素作为家里备用药,在A、B、C、D各一盒中随机购买两盒,请用画树状图或列表法求出他刚好选中A和B的概率.
 如图,已知双曲线y=$\frac{k}{x}$(k>0)经过Rt△OAB的直角边AB的中点C,与斜边OB相交于点D,若OD=1,则BD=$\sqrt{2}$-1.
如图,已知双曲线y=$\frac{k}{x}$(k>0)经过Rt△OAB的直角边AB的中点C,与斜边OB相交于点D,若OD=1,则BD=$\sqrt{2}$-1. 如图,正六边形ABCDEF内接于半径为3的圆O,则劣弧AB的长度为π.
如图,正六边形ABCDEF内接于半径为3的圆O,则劣弧AB的长度为π.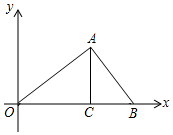 在如图所示的直角坐标系xOy中,AC⊥OB,OA⊥AB,OB=3,点C是OB上靠近O点的三等分点,若反比例函数y=$\frac{k}{x}$(x>0)的图象(图中未画出)与△OAB有两个交点,则k的取值范围是0<k<$\frac{9}{8}\sqrt{2}$.
在如图所示的直角坐标系xOy中,AC⊥OB,OA⊥AB,OB=3,点C是OB上靠近O点的三等分点,若反比例函数y=$\frac{k}{x}$(x>0)的图象(图中未画出)与△OAB有两个交点,则k的取值范围是0<k<$\frac{9}{8}\sqrt{2}$.