题目内容
3. 如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{6}{x}$相交于A,B两点,C是第一象限内双曲线上一点,连接CA并延长交y轴于点P,连接BP,BC.若△PBC的面积是24,则点C的坐标为(6,1).
如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{6}{x}$相交于A,B两点,C是第一象限内双曲线上一点,连接CA并延长交y轴于点P,连接BP,BC.若△PBC的面积是24,则点C的坐标为(6,1).
分析 设C点坐标为(a,$\frac{6}{a}$),根据反比例函数与一次函数的交点问题解方程组求得A点坐标为(2,3),B点坐标为(-2,-3),再利用待定系数法确定直线BC的解析式,直线AC的解析式,于是利用y轴上点的坐标特征得到D、P点坐标,然后利用S△PBC=S△PBD+S△CPD得到关于a的方程,求出a的值即可得到C点坐标.
解答 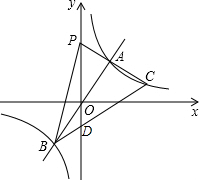 解:设BC交y轴于D,如图,设C点坐标为(a,$\frac{6}{a}$)
解:设BC交y轴于D,如图,设C点坐标为(a,$\frac{6}{a}$)
解方程组$\left\{\begin{array}{l}{y=\frac{3}{2}x}\\{y=\frac{6}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=-3}\end{array}\right.$,
∴A点坐标为(2,3),B点坐标为(-2,-3),
设直线BC的解析式为y=kx+b,
把B(-2,-3)、C(a,$\frac{6}{a}$)代入得$\left\{\begin{array}{l}{-2k+b=-3}\\{ak+b=\frac{6}{a}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{3}{a}}\\{b=\frac{6}{a}-3}\end{array}\right.$,
∴直线BC的解析式为y=$\frac{3}{a}$x+$\frac{6}{a}$-3,
当x=0时,y=$\frac{3}{a}$x+$\frac{6}{a}$-3=$\frac{6}{a}$-3,
∴D点坐标为(0,$\frac{6}{a}$-3)
设直线AC的解析式为y=mx+n,
把A(2,3)、C(a,$\frac{6}{a}$)代入得$\left\{\begin{array}{l}{2m+n=3}\\{am+n=\frac{6}{a}}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-\frac{3}{a}}\\{n=\frac{6}{a}+3}\end{array}\right.$,
∴直线AC的解析式为y=-$\frac{3}{a}$x+$\frac{6}{a}$+3,
当x=0时,y=-$\frac{3}{a}$x+$\frac{6}{a}$+3=$\frac{6}{a}$+3,
∴P点坐标为(0,$\frac{6}{a}$+3)
∴PD=($\frac{6}{a}$+3)-($\frac{6}{a}$-3)=6,
∵S△PBC=S△PBD+S△CPD,
∴$\frac{1}{2}$×2×6+$\frac{1}{2}$×a×6=24,解得a=6,
∴C点坐标为(6,1).
故答案为:(6,1).
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点;若方程组无解则两者无交点.也考查了用待定系数法求一次函数的解析式.

| A. | $\frac{6800}{x}$-6=$\frac{6800}{x+34}$+4 | B. | $\frac{6800}{x}$+6=$\frac{6800}{x+34}$-4 | ||
| C. | $\frac{6800}{x+34}$-6=$\frac{6800}{x}$+4 | D. | $\frac{6800}{x+34}$+6=$\frac{6800}{x}$-4 |
| A. | 3cm | B. | 11cm | C. | 20cm | D. | 24cm |
| A. | x≠-3 | B. | x>-3 | C. | x≥-3 | D. | x≤-3 |
 如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ACF=48°,则∠ABC的度数为( )
如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ACF=48°,则∠ABC的度数为( )| A. | 48° | B. | 36° | C. | 30° | D. | 24° |
| A. | 2.600<x≤2.605 | B. | 2.595<x≤2.605 | C. | 2.595≤x<2.605 | D. | 2.50≤x<2.70 |
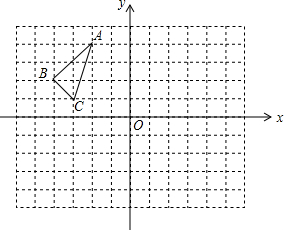 如图所示,把△ABC置于平面直角坐标系中,请你按下列要求分别画图:
如图所示,把△ABC置于平面直角坐标系中,请你按下列要求分别画图: