题目内容
11.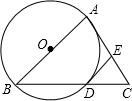 如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点D,E是AC的中点,判断DE与⊙O的位置关系,并说明理由.
如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点D,E是AC的中点,判断DE与⊙O的位置关系,并说明理由.
分析 连接OE、OD,根据切线的性质得到∠BAC=90°,根据三角形中位线定理和三角形全等的判定定理证明△AOE≌△DOE,得到∠ODE=∠BAC=90°,根据切线的判定定理证明结论.
解答 答: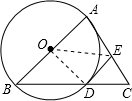 DE与⊙O相切,
DE与⊙O相切,
证明:连接OE、OD,
∵AC是⊙O的切线,
∴∠BAC=90°,
∵OA=OB,AE=EC,
∴OE∥BC,
∴∠AOE=∠B,∠EOD=∠ODB,
∵OA=OB,
∴∠B=∠ODB,
∴∠AOE=∠EOD,
在△AOE和△DOE中,
$\left\{\begin{array}{l}{OA=OD}\\{∠AOE=∠DOE}\\{OE=OE}\end{array}\right.$,
∴△AOE≌△DOE,
∴∠ODE=∠BAC=90°,
∴DE与⊙O相切.
点评 本题考查的是直线与圆的位置关系,掌握切线的性质定理和判定定理是解题的关键,注意要正确作出辅助线.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
19.若要从二次函数y=3x2的图象得到二次函数y=3(x+2)2-1的图象,则二次函数y=3x2的图象必须( )
| A. | 上移1个单位,右移2个单位 | B. | 下移1个单位,右移2个单位 | ||
| C. | 下移1个单位,左移2个单位 | D. | 上移2个单位,右移1个单位 |
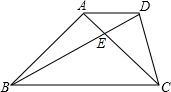 如图,已知梯形ABCD,AD∥BC,BD=BC,AB=AC,∠BAC=90°.求:sin∠DBC.
如图,已知梯形ABCD,AD∥BC,BD=BC,AB=AC,∠BAC=90°.求:sin∠DBC. 如图,已知△ABC是等边三角形,将△ABC绕点A逆时针方向旋转20°,得到△ADE,BD和EC所在直线相交于点O.求∠BOE的度数.
如图,已知△ABC是等边三角形,将△ABC绕点A逆时针方向旋转20°,得到△ADE,BD和EC所在直线相交于点O.求∠BOE的度数.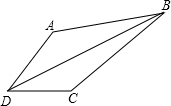 在四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=DC,若AB=5,BC=4,求BD的长.
在四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=DC,若AB=5,BC=4,求BD的长.