题目内容
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,令x0=
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,令x0=| b |
| 2a |
考点:二次函数图象与系数的关系
专题:
分析:①根据二次函数开口方向可判断a的正负;
②由对称轴大于0可判断b的正负;
③由于二次函数交于y轴负半轴可判断c的正负;
④先分别判断ab与b+c的符号,再根据平面直角坐标系内各象限点的坐标特征即可判断点(ab,b+c)所在的象限;
⑤由二次函数的增减性即可判断;
⑥根据二次函数的性质结合图象即可判断.
②由对称轴大于0可判断b的正负;
③由于二次函数交于y轴负半轴可判断c的正负;
④先分别判断ab与b+c的符号,再根据平面直角坐标系内各象限点的坐标特征即可判断点(ab,b+c)所在的象限;
⑤由二次函数的增减性即可判断;
⑥根据二次函数的性质结合图象即可判断.
解答:解:①∵二次函数开口向上,∴a>0,故①正确;
②∵对称轴为-
>0,且a>0,∴b<0,故②正确;
③∵二次函与y轴负半轴相交,∴c<0,故③正确;
④∵a>0,b<0,∴ab<0,
∵b<0,c<0,∴b+c<0,
∴点(ab,b+c)在第三象限,故④错误;
⑤∵y=ax2+bx+c=a(x+
)2+
,x0=
<0<-
,
∴当x0=
<x<-
时,y随x的增大而减小;当x>-
时,y随x的增大而增大;故⑤错误;
⑥∵a>0,∴图象有最低点,即y有最小值,
∵顶点在第四象限,∴最小值为负数,故⑥正确.
故答案为①②③⑥.
②∵对称轴为-
| b |
| 2a |
③∵二次函与y轴负半轴相交,∴c<0,故③正确;
④∵a>0,b<0,∴ab<0,
∵b<0,c<0,∴b+c<0,
∴点(ab,b+c)在第三象限,故④错误;
⑤∵y=ax2+bx+c=a(x+
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
∴当x0=
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
⑥∵a>0,∴图象有最低点,即y有最小值,
∵顶点在第四象限,∴最小值为负数,故⑥正确.
故答案为①②③⑥.
点评:本题考查了二次函数图象与系数的关系,对于二次函数y=ax2+bx+c(a≠0)来说,
①二次项系数a决定抛物线的开口方向和大小.
当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;
②一次项系数b和二次项系数a共同决定对称轴的位置.
当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异);
③常数项c决定抛物线与y轴交点,抛物线与y轴交于(0,c).
④抛物线与x轴交点个数.
△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.
①二次项系数a决定抛物线的开口方向和大小.
当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;
②一次项系数b和二次项系数a共同决定对称轴的位置.
当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异);
③常数项c决定抛物线与y轴交点,抛物线与y轴交于(0,c).
④抛物线与x轴交点个数.
△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
近年来,全国各地房价不断上涨,我市2011年12月份的房价平均每平方米为12400元,比2009年同期的房价平均每平方米上涨了5800元.假设这两年我市房价的平均增长率为x,则由题意可列出关于x的方程为( )
| A、(1+x)2=12400 |
| B、5800(1+x)2=12400 |
| C、(12400-5800)(1+x)=12400 |
| D、(12400-5800)(1+x)2=12400 |
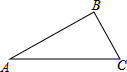 如图△ABC是一个直三棱柱的俯视图,若该直三棱柱的高10cm,∠A=30°,∠C=45°,BC=2
如图△ABC是一个直三棱柱的俯视图,若该直三棱柱的高10cm,∠A=30°,∠C=45°,BC=2| 2 |
A、(42+22
| ||||
B、(22+42
| ||||
C、(44+24
| ||||
D、(60+20
|
 如图,正方形EFGH的外接圆⊙O是正方形ABCD的内切圆,试求AB:EF的值.
如图,正方形EFGH的外接圆⊙O是正方形ABCD的内切圆,试求AB:EF的值.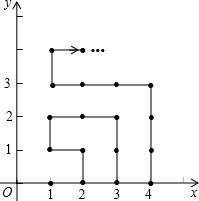 如图,在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,其顺序按图中点的坐标分别为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…的规律排列,根据这个规律,第2015个点的横坐标为
如图,在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,其顺序按图中点的坐标分别为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…的规律排列,根据这个规律,第2015个点的横坐标为