Question

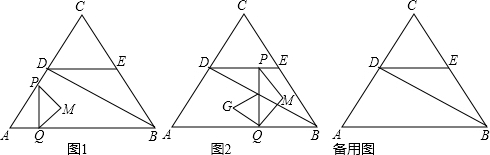
15．一斜坡上有一高尔夫球场．斜坡的坡度为i=1：10．一球从斜坡底部O点被击起，飞行轨道是一条抛物线，轨迹最高点H离开O点的水平面高度是8米，离O点的水平距离是4米．则该球落地点A与O点的距离为$\frac{39\sqrt{101}}{50}$（结果保留根号）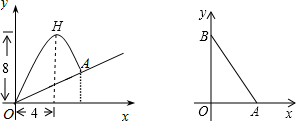

Answer 1

分析 由顶点式和待定系数法求出抛物线解析式，把A点的坐标代入求出b的值，再由勾股定理求出OA的长即可．

解答 解：∵抛物线顶点坐标为（4，8），
∴设抛物线解析式为y=a（x-4）²+8，
把（0，0）代入得：16a+8=0，解得：a=-$\frac{1}{2}$，
∴抛物线解析式为y=-$\frac{1}{2}$（x-4）²+8=-$\frac{1}{2}{x}^{2}$+4x，
∵斜坡的坡度为i=1：10，
∴设A的坐标为（10b，b），代入抛物线得：-$\frac{1}{2}$×100b²+40b=b，
解得：b=$\frac{39}{50}$或b=0（舍去），
由勾股定理得：OA=$\sqrt{（10b）^{2}+{b}^{2}}$=$\sqrt{101}b$=$\frac{39\sqrt{101}}{50}$；
故答案为：$\frac{39\sqrt{101}}{50}$．

点评 本题考查了d待定系数法求二次函数的解析式、二次函数的应用、解直角三角形-坡度角问题；求出二次函数的解析式是解决问题的关键．