题目内容
 如图,抛物线y=a(x-1)2+4与x轴交于点A、B,与y轴交于点C,抛物线的顶点为D,连接BD、BC,已知点A的坐标为(-1,0).
如图,抛物线y=a(x-1)2+4与x轴交于点A、B,与y轴交于点C,抛物线的顶点为D,连接BD、BC,已知点A的坐标为(-1,0).(1)求该抛物线的解析式;
(2)求△BCD的面积.
考点:抛物线与x轴的交点
专题:
分析:(1)把点A的坐标(-1,0)代入y=a(x-1)2+4可求出a的值,进而可求出抛物线的解析式;
(2)根据B、C点的坐标求得直线BC的解析式,则可以求得对称轴与直线BC的交点E的坐标,易求DE的长度;由三角形的面积公式进行解答即可.
(2)根据B、C点的坐标求得直线BC的解析式,则可以求得对称轴与直线BC的交点E的坐标,易求DE的长度;由三角形的面积公式进行解答即可.
解答: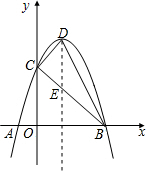 解:(1)把点A的坐标为(-1,0)代入y=a(x-1)2+4,得
解:(1)把点A的坐标为(-1,0)代入y=a(x-1)2+4,得
a(-1-1)2+4=0
解得a=-1.
则该抛物线解析式为:y=-(x-1)2+4;
(2)如图,设直线BC与对称轴交于点E.
∵抛物线的解析式为y=a(x-1)2+4,
∴顶点坐标是(1,4),对称轴为x=1,且C(0,4).
又∵点A的坐标为(-1,0),
∴B(3,0).
设直线BC的解析式为y=kx+b(k≠0),则
,
解得
.
则直线BC的解析式为:y=-
x+4.
∴
,
解得
,
∴E(1,
),
∴DE=4-
=
.
则△BCD的面积=
DE•OB=
×
×3=2,即△BCD的面积是2.
 解:(1)把点A的坐标为(-1,0)代入y=a(x-1)2+4,得
解:(1)把点A的坐标为(-1,0)代入y=a(x-1)2+4,得a(-1-1)2+4=0
解得a=-1.
则该抛物线解析式为:y=-(x-1)2+4;
(2)如图,设直线BC与对称轴交于点E.
∵抛物线的解析式为y=a(x-1)2+4,
∴顶点坐标是(1,4),对称轴为x=1,且C(0,4).
又∵点A的坐标为(-1,0),
∴B(3,0).
设直线BC的解析式为y=kx+b(k≠0),则
|
解得
|
则直线BC的解析式为:y=-
| 4 |
| 3 |
∴
|
解得
|
∴E(1,
| 8 |
| 3 |
∴DE=4-
| 8 |
| 3 |
| 4 |
| 3 |
则△BCD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
点评:本题考查了抛物线与x轴的交点.解答(2)题时,涉及到了待定系数法求一次函数解析式,抛物线的性质以及三角形的面积求法.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
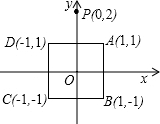 在平面直角坐标系中,正方形ABCD的顶点分别为A(1,1)、B(1,-1)、C(-1,-1)、D(-1,1),y轴上有一点P(0,2),作点P关于点A的对称点P1,作P1关于点B的对称点P2作点P2关于点C的对称点P3,作P3关于点D的对称点P4,作点P4关于点A的对称点P5,作P5关于点B的对称点P6┅,按如此操作下去,则点P2015的坐标为( )
在平面直角坐标系中,正方形ABCD的顶点分别为A(1,1)、B(1,-1)、C(-1,-1)、D(-1,1),y轴上有一点P(0,2),作点P关于点A的对称点P1,作P1关于点B的对称点P2作点P2关于点C的对称点P3,作P3关于点D的对称点P4,作点P4关于点A的对称点P5,作P5关于点B的对称点P6┅,按如此操作下去,则点P2015的坐标为( ) 如图,抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若该抛物线与x轴的一个交点为P(4,0),则另一个交点坐标为
如图,抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若该抛物线与x轴的一个交点为P(4,0),则另一个交点坐标为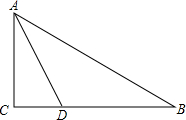 已知如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D,
已知如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D, 如图,已知线段ab(a>b).
如图,已知线段ab(a>b). 如图,四边形ABCD是长方形(长方形对边相等且平行,四个角为直角),
如图,四边形ABCD是长方形(长方形对边相等且平行,四个角为直角),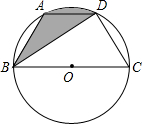 如图,已知点A、B、C、D均在半径为3的已知圆上,AD∥BC,BD平分∠ABC,∠C=60°.
如图,已知点A、B、C、D均在半径为3的已知圆上,AD∥BC,BD平分∠ABC,∠C=60°. 如图,有一块半圆形钢板,直径AB=20cm,计划将此钢板切割成四边形ABCD,CD∥AB,C,D两点在圆周上,且CD=10cm.
如图,有一块半圆形钢板,直径AB=20cm,计划将此钢板切割成四边形ABCD,CD∥AB,C,D两点在圆周上,且CD=10cm.