题目内容
8.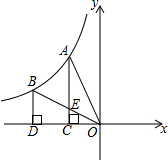 如图,反比例函数y=$\frac{k}{x}(k≠0)$的图象经过A、B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为1,则k的值为-$\frac{8}{3}$.
如图,反比例函数y=$\frac{k}{x}(k≠0)$的图象经过A、B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为1,则k的值为-$\frac{8}{3}$.
分析 先设点B坐标为(a,b),根据平行线分线段成比例定理,求得梯形BDCE的上下底边长与高,再根据四边形BDCE的面积求得ab的值,最后计算k的值.
解答  解:设点B坐标为(a,b),则DO=-a,BD=b
解:设点B坐标为(a,b),则DO=-a,BD=b
∵AC⊥x轴,BD⊥x轴
∴BD∥AC
∵OC=CD
∴CE=$\frac{1}{2}$BD=$\frac{1}{2}$b,CD=$\frac{1}{2}$DO=$\frac{1}{2}$a,
∵四边形BDCE的面积为1,
∴$\frac{1}{2}$(BD+CE)×CD=1,即$\frac{1}{2}$(b+$\frac{1}{2}$b)×(-$\frac{1}{2}$a)=1,
∴ab=-$\frac{8}{3}$,
将B(a,b)代入反比例函数$\frac{k}{x}(k≠0)$,得
k=ab=-$\frac{8}{3}$.
故答案为:-$\frac{8}{3}$.
点评 本题主要考查了反比例函数系数k的几何意义,解决问题的关键是运用数形结合的思想方法进行求解.本题也可以根据△OCE与△ODB相似比为1:2求得△BOD的面积,进而得到k的值.

练习册系列答案
相关题目
16.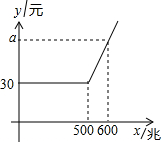 如图是某通讯公司的4G上网套餐每月上网费用y(单位:元)与上网流量x(单位;兆)之间函数关系的图象.若该公司每户每月上网流量超过500兆以后,每兆流量需加收0.29元.则图中a的值为( )
如图是某通讯公司的4G上网套餐每月上网费用y(单位:元)与上网流量x(单位;兆)之间函数关系的图象.若该公司每户每月上网流量超过500兆以后,每兆流量需加收0.29元.则图中a的值为( )
 如图是某通讯公司的4G上网套餐每月上网费用y(单位:元)与上网流量x(单位;兆)之间函数关系的图象.若该公司每户每月上网流量超过500兆以后,每兆流量需加收0.29元.则图中a的值为( )
如图是某通讯公司的4G上网套餐每月上网费用y(单位:元)与上网流量x(单位;兆)之间函数关系的图象.若该公司每户每月上网流量超过500兆以后,每兆流量需加收0.29元.则图中a的值为( )| A. | 140 | B. | 174 | C. | 59 | D. | 69 |
3.有一枚均匀的正方体骰子,骰子各个面上的点数分别为1,2,3,4,5,6,若任意抛掷一次骰子,朝上的面的点数记为x,计算|x-3|,则其结果恰为1的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
20.下列说法中,正确的是( )
| A. | 将一组数据中的每一个数据都加同一个正数,方差变大 | |
| B. | 为了解全市同学对书法课的喜欢情况,调查了某校所有女生 | |
| C. | “任意画出一个矩形,它是轴对称图形”是必然事件 | |
| D. | 为了审核书稿中的错别字,选择抽样调查 |
18.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,随机摸出一个小球后不放回,再随机摸出一个小球,则两次摸出的小球标号之和等于5的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
 如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E,则∠DOE的度数为90°.
如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E,则∠DOE的度数为90°.