题目内容
3.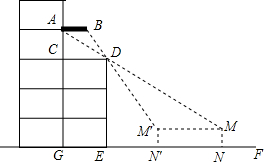 周末,小凯和同学带着皮尺,去测量杨大爷家露台遮阳篷的宽度.如图,由于无法直接测量,小凯便在楼前地面上选择了一条直线EF,通过在直线EF上选点观侧,发现当他位于N点时,他的视线从M点通过露台D点正好落在遮阳篷A点处;当他位于N′点时,视线从M′点通过D点正好落在遮阳篷B点处,这样观测到的两个点A、B间的距离即为遮阳篷的宽.已知AB∥CD∥EF,点C在AG上,AG、DE、MN、M′N′均垂直于EF,MN=M′N′,露台的宽CD=GE.测得CE=5米,EN=12.3米,NN′=6.2米.请你根据以上信息,求出遮阳篷的宽AB是多少米?(结果精确到0.01米)
周末,小凯和同学带着皮尺,去测量杨大爷家露台遮阳篷的宽度.如图,由于无法直接测量,小凯便在楼前地面上选择了一条直线EF,通过在直线EF上选点观侧,发现当他位于N点时,他的视线从M点通过露台D点正好落在遮阳篷A点处;当他位于N′点时,视线从M′点通过D点正好落在遮阳篷B点处,这样观测到的两个点A、B间的距离即为遮阳篷的宽.已知AB∥CD∥EF,点C在AG上,AG、DE、MN、M′N′均垂直于EF,MN=M′N′,露台的宽CD=GE.测得CE=5米,EN=12.3米,NN′=6.2米.请你根据以上信息,求出遮阳篷的宽AB是多少米?(结果精确到0.01米)
分析 延长MM′交DE于H,如图,易得HM=EN=12.3米,CD=GE=5米,MM′=NN′=6.2米,先证明Rt△ACD∽Rt△DHM,则根据相似三角形的性质得$\frac{AD}{DM}$=$\frac{CD}{HM}$=$\frac{5}{12.3}$,再证明△ABD∽△MM′D,则利用相似比得到$\frac{AB}{6.2}$=$\frac{5}{12.3}$,然后利用比例性质求AB即可.
解答 解:延长MM′交DE于H,如图,则HM=EN=12.3米,CD=GE=5米,MM′=NN′=6.2米,
∵CD∥HM,
∴∠ADC=∠DMH,
∴Rt△ACD∽Rt△DHM,
∴$\frac{AD}{DM}$=$\frac{CD}{HM}$=$\frac{5}{12.3}$,
∵AB∥MM′,
∴△ABD∽△MM′D,
∴$\frac{AB}{MM′}$=$\frac{AD}{DM}$=$\frac{5}{12.3}$,即$\frac{AB}{6.2}$=$\frac{5}{12.3}$,解得AB≈2.52(米).
答:遮阳篷的宽AB是2.52米.
点评 本题考查了相似三角形的应用:利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度或宽度.

练习册系列答案
相关题目
15.下列分式的值,可以为零的是( )
| A. | $\frac{{x}^{2}+1}{x-1}$ | B. | $\frac{x+1}{{x}^{2}-1}$ | C. | $\frac{{x}^{2}+2x+1}{x+1}$ | D. | $\frac{x+1}{x-1}$ |
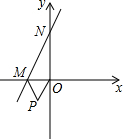 如图,已知直线y=2x+6与x轴、y轴分别交于M,N两点,以OM为边在x轴下方作等边三角形OMP,现将△OMP沿y轴向上平移,当点P恰好落在直线MN上时,点P运动的路程为$\frac{3}{2}$$\sqrt{3}$+3.
如图,已知直线y=2x+6与x轴、y轴分别交于M,N两点,以OM为边在x轴下方作等边三角形OMP,现将△OMP沿y轴向上平移,当点P恰好落在直线MN上时,点P运动的路程为$\frac{3}{2}$$\sqrt{3}$+3.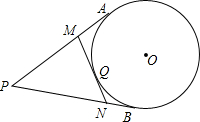 如图,PA、PB是⊙O的切线,Q为$\widehat{AB}$上一点,过点Q的直线MN与⊙O相切,已知PA=4,则△PMN周长=8.
如图,PA、PB是⊙O的切线,Q为$\widehat{AB}$上一点,过点Q的直线MN与⊙O相切,已知PA=4,则△PMN周长=8.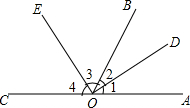 ∠AOB与∠BOC互为补角,OD平分∠AOB,∠3+∠2=90°,如图所示.求证∠BOE=$\frac{1}{2}$∠BOC.请完成下列证明.
∠AOB与∠BOC互为补角,OD平分∠AOB,∠3+∠2=90°,如图所示.求证∠BOE=$\frac{1}{2}$∠BOC.请完成下列证明.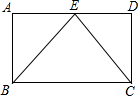 如图所示,在?ABCD中,E为AD的中点,△CBE是等边三角形,求证:?ABCD是矩形.
如图所示,在?ABCD中,E为AD的中点,△CBE是等边三角形,求证:?ABCD是矩形.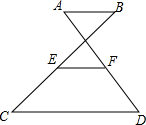 如图,AB∥CD,点E是BC的中点,点F是AD的中点,若AB=5,CD=12,求EF的长.
如图,AB∥CD,点E是BC的中点,点F是AD的中点,若AB=5,CD=12,求EF的长.