题目内容
14.正多边形的一个内角为120°,则该多边形对称轴的条数为( )| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
分析 一个正多边形的每个内角都相等,根据内角与外角互为邻补角,因而就可以求出外角的度数.根据任何多边形的外角和都是360度,利用360除以外角的度数就可以求出外角和中外角的个数,即多边形的边数.
解答  解:外角是180°-120°=60°,
解:外角是180°-120°=60°,
360°÷60°=6,则这个多边形是六边形.
则正六边形的对称轴有6条.
故选:B.
点评 考查了轴对称的性质,多边形内角与外角,根据外角和的大小与多边形的边数无关,由外角和求正多边形的边数,是常见的题目,需要熟练掌握.另外,要记住偶数边的正多边形既是轴对称图形,又是中心对称图形,奇数边的正多边形只是轴对称图形.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
19.已知Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式中正确的是( )
| A. | sinA=$\frac{2}{3}$ | B. | cosA=$\frac{2}{3}$ | C. | tanA=$\frac{2}{3}$ | D. | cotA=$\frac{2}{3}$ |
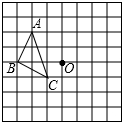 如图,在正方形网格上有一个△ABC.
如图,在正方形网格上有一个△ABC.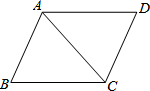 如图,在平行四边形ABCD中,BC=10,sin∠ACB=$\frac{4}{5}$,AC=BC,则平行四边形ABCD的面积是80.
如图,在平行四边形ABCD中,BC=10,sin∠ACB=$\frac{4}{5}$,AC=BC,则平行四边形ABCD的面积是80.