题目内容
9.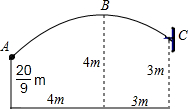 一场篮球赛中,球员甲跳起投篮,已知球在A处出手时离地面$\frac{20}{9}$m,与篮筐中心C的水平距离为7m,当球运行的水平距离是4m时,达到最大高度4m(B处),篮筐距地面3m,篮球运行的路线为抛物线(如图所示).
一场篮球赛中,球员甲跳起投篮,已知球在A处出手时离地面$\frac{20}{9}$m,与篮筐中心C的水平距离为7m,当球运行的水平距离是4m时,达到最大高度4m(B处),篮筐距地面3m,篮球运行的路线为抛物线(如图所示).(1)建立适当的平面直角坐标系,并求出抛物线的解析式;
(2)判断此球能否投中?
分析 (1)建立适当的平面直角坐标系,根据已知条件即可得到结论;
(2)根据(1)中的篮球运动抛物线的解析式,把坐标(7,3)代入判断是否满足,则即可确定篮球是否能准确投中.
解答 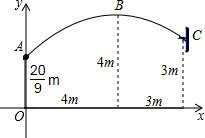 解:(1)过A作水平线的垂线,垂直为O,以O为坐标原点,直线OA为y轴,建立平面直角坐标系,由题意得A(0,$\frac{20}{9}$),顶点B(4,4),
解:(1)过A作水平线的垂线,垂直为O,以O为坐标原点,直线OA为y轴,建立平面直角坐标系,由题意得A(0,$\frac{20}{9}$),顶点B(4,4),
设抛物线的解析式为y=a(x-4)2+4,
∴$\frac{20}{9}$=a(x-4)2+4.
解得:a=-$\frac{1}{9}$.
∴抛物线的解析式为:y=-$\frac{1}{9}$(x-4)2+4;
(2)当x=7时,y=-$\frac{1}{9}$(7-4)2+4=3,
∵点(7,3)在抛物线上,
∴球能准确投中.
点评 本题考查了二次函数在实际生活中的应用,待定系数法求函数的解析式,正确的求得函数的解析式是解题的关键.

练习册系列答案
相关题目
19.已知Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式中正确的是( )
| A. | sinA=$\frac{2}{3}$ | B. | cosA=$\frac{2}{3}$ | C. | tanA=$\frac{2}{3}$ | D. | cotA=$\frac{2}{3}$ |
20.巡道员沿东西方向的铁路进行巡视维护,他从驻地出发,先向东行走7km,休息之后继续向东行走2km,然后折返向西行走12.5km,用有理数的相关知识回答;此时他在驻地的什么方向?与驻地的距离是多少?
17.将边长为1的正方形纸片如图1所示的方法进行对折,记第一次对折后得到的图形面积为 S1,第2次对折后得到的图形面积为S2…,第n次对折后得到的图形面积为Sn,请根据图2化简S1+S2+S3…S2014=( )
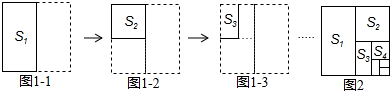

| A. | 1-$\frac{1}{{{2^{2015}}}}$ | B. | $\frac{2014}{2015}$ | C. | 1-$\frac{1}{{{2^{2014}}}}$ | D. | $\frac{2013}{2014}$ |
14.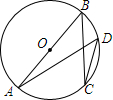 如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )
如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )
 如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )
如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )| A. | $\frac{{8\sqrt{13}}}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{{24\sqrt{5}}}{5}$ | D. | 12 |
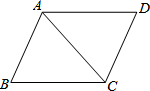 如图,在平行四边形ABCD中,BC=10,sin∠ACB=$\frac{4}{5}$,AC=BC,则平行四边形ABCD的面积是80.
如图,在平行四边形ABCD中,BC=10,sin∠ACB=$\frac{4}{5}$,AC=BC,则平行四边形ABCD的面积是80.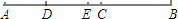 如图,已知点C为AB上一点,AC=24cm,CB=$\frac{2}{3}$AC,D、E分别为AC、AB的中点,求DE的长.
如图,已知点C为AB上一点,AC=24cm,CB=$\frac{2}{3}$AC,D、E分别为AC、AB的中点,求DE的长.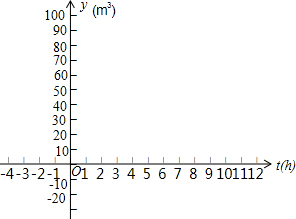 某水池的容积为90m3,水池中已有水10m3,现按8m3/h的流量向水池中注水.
某水池的容积为90m3,水池中已有水10m3,现按8m3/h的流量向水池中注水.