题目内容
3.若抛物线y=ax2+bx+c(a≠0)的顶点在第一象限,且过点(0,1)和(-1,0),设t=a+b+c,则t的取值范围是( )| A. | 0<t<1 | B. | 0<t<2 | C. | 1<t<2 | D. | -1<t<1 |
分析 由抛物线的顶点在第一象限及过点(0,1)和(-1,0),即可得出-1<a<0、0<b<1,再由t=a+b+c=2b,即可得出t的取值范围.
解答 解:∵抛物线y=ax2+bx+c(a≠0)的顶点在第一象限,且过点(0,1)和(-1,0),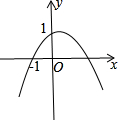
∴$\left\{\begin{array}{l}{a<0}\\{c=1}\\{a-b+c=0}\\{-\frac{b}{2a}>0}\end{array}\right.$,
∴b=a+1>0,
∴-1<a<0,0<b<1.
∵t=a+b+c=2b,
∴0<t<2.
故选B.
点评 本题考查了二次函数图象与系数的关系以及二次函数图象上点的坐标特征,依照题意画出函数图象,利用数形结合是解题的关键.

练习册系列答案
相关题目
14.二次函数y=2(x+2)2-4的最小值是( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
8.已知P=m2-m,Q=m-2,则P与Q的大小关系为( )
| A. | P>Q | B. | P=Q | C. | P<Q | D. | 无法确定 |