题目内容
已知在△ABC中,AC=10,AB=21,BC=17,求tanA.
考点:解直角三角形,勾股定理
专题:
分析:过C作CD⊥AB于D,设AD=a,则BD=21-a,在Rt△ADC和Rt△CDB中,由勾股定理得出方程102-a2=172-(21-a)2,求出a,即可求出AD和CD,解直角三角形即可.
解答:
解:过C作CD⊥AB于D,
设AD=a,则BD=21-a,
在Rt△ADC和Rt△CDB中,由勾股定理得:CD2=AC2-AD2=BC2-BD2,
∵AC=10,AB=21,BC=17,
∴102-a2=172-(21-a)2,
解得:a=6,
即AD=6,由勾股定理得:CD=
=8,
tanA=
=
=
.

解:过C作CD⊥AB于D,
设AD=a,则BD=21-a,
在Rt△ADC和Rt△CDB中,由勾股定理得:CD2=AC2-AD2=BC2-BD2,
∵AC=10,AB=21,BC=17,
∴102-a2=172-(21-a)2,
解得:a=6,
即AD=6,由勾股定理得:CD=
| 102-62 |
tanA=
| CD |
| AD |
| 8 |
| 6 |
| 4 |
| 3 |
点评:本题考查了解直角三角形和勾股定理的应用,解此题的关键是构造直角三角形,题目比较好,难度适中.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
用一个平面去截圆柱体,则截面形状不可能是( )
| A、梯形 | B、正方形 | C、长方形 | D、圆 |
下列说法错误的是( )
| A、一个三角形中至少有一个角不少于60° |
| B、三角形的中线不可能在三角形的外部 |
| C、三角形的中线把三角形的面积平均分成相等的两部分 |
| D、直角三角形只有一条高 |
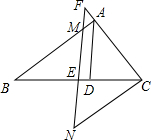 如图,AD为△ABC的角平分线,E为BC的中点,过E作EF∥AD,交AB于点M,交CA的延长线F,CN∥AB交FE的延长线于N,求证:BM=CF.
如图,AD为△ABC的角平分线,E为BC的中点,过E作EF∥AD,交AB于点M,交CA的延长线F,CN∥AB交FE的延长线于N,求证:BM=CF. △ABC中,AB=61cm,BC=22cm,BC边上的中线AD=60cm,试说明△ABC是等腰三角形.
△ABC中,AB=61cm,BC=22cm,BC边上的中线AD=60cm,试说明△ABC是等腰三角形.