题目内容
2.在⊙O中,点A,B,C,E在⊙O中,点D为弦AB上一点,连接BE,CE,AC,若BD=CD,CD∥BE.(1)如图1,求证:CE=AC;
(2)若点D与O重合,如图2,连接AE、BC,作EH⊥BC于H,CK⊥AB于K,求证:AE=2HK.
(3)在(2)的条件下,如图2,BK=3HK,EC=4$\sqrt{10}$,求BH长.

分析 (1)如图1中,连接BC.只要证明∠EBC=∠CBA,推出$\widehat{EC}$=$\widehat{AC}$,即可证明.
(2)如图2中,延长CK交⊙O于F,连接EF交BC于H′,连接AF.利用同一法证明H与H′重合,再证明AE=CF,CF=2HK即可.
(3)利用tan∠CBA=$\frac{1}{3}$,求出BC、AB、CK,在Rt△CHF中,利用tan∠CFH=$\frac{1}{3}$,求出CH即可解决问题.
解答 证明:(1)如图1中,连接BC.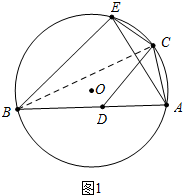
∵BD=DC,
∴∠DBC=∠DCB,
∵CD∥BE,
∴∠EBC=∠BCD,
∴∠EBC=∠CBD,
∴$\widehat{EC}$=$\widehat{AC}$,
∴EC=AC.
(2)如图2中,延长CK交⊙O于F,连接EF交BC于H′,连接AF.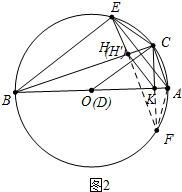
∵∠EBC=∠EFC,∠BEF=∠FAB,
∵$\widehat{EC}$=$\widehat{AC}$,
∴∠EFC=∠CFA,
∵∠AFK+∠FAB=90°,
∴∠EBC+∠AEF=90°,
∴∠BH′E=90°,
∴EH′⊥BC,∵EH⊥BC,
∴H与H′重合,
∵AB⊥CF,
∴CK=KF,$\widehat{AC}$=$\widehat{AF}$,
∴$\widehat{AE}$=$\widehat{CF}$,
∴AE=CF,
在Rt△CHF中,HK=$\frac{1}{2}$CF,
∴AE=CF=2HK.
(3)∵BK=3HK=3CK,
∴tan∠CBA=$\frac{CK}{BK}$=$\frac{1}{3}$=$\frac{AC}{BC}$,
∵AC=CE=4$\sqrt{10}$,
∴BC=12$\sqrt{10}$,
∵AB是直径,
∴∠BCA=90°,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{(12\sqrt{10})^{2}+(4\sqrt{10})^{2}}$=40,
∵$\frac{1}{2}$•AB•CK=$\frac{1}{2}$•BC•AC,
∴CK=$\frac{BC•AC}{AB}$=12,
∴CF=2CF=24,
∵tan∠CFH=tan∠CBA=$\frac{CH}{FH}$=$\frac{1}{3}$,设HC=a,FH=3a,
∴a2+(3a)2=242,
∴a=$\frac{12\sqrt{10}}{5}$,
∴HC=$\frac{12\sqrt{10}}{5}$,
∴BH=BC-CH=12$\sqrt{10}$-$\frac{12\sqrt{10}}{5}$=$\frac{48\sqrt{10}}{5}$.
点评 本题考查圆综合题、垂径定理、平行线的性质、锐角三角函数、勾股定理等知识,解题的关键是灵活应用锐角三角函数解决问题,学会利用同一法证明H与H′重合,学会添加常用辅助线,属于中考压轴题.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案 如图,已知直线AB与CD相交于O,OE、OF分别是∠BOD、AOD平分线,
如图,已知直线AB与CD相交于O,OE、OF分别是∠BOD、AOD平分线,
 如图,在?ABCD中,∠BAD的平分线交BC于点E,∠BCD的平分线交AD于点F.
如图,在?ABCD中,∠BAD的平分线交BC于点E,∠BCD的平分线交AD于点F.