题目内容
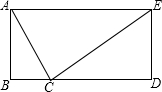 已知:如图,C是线段BD上一点,AB⊥BD,ED⊥BD,∠ACE=90°,tan∠ACB=2,AB=4,ED=3.求:
已知:如图,C是线段BD上一点,AB⊥BD,ED⊥BD,∠ACE=90°,tan∠ACB=2,AB=4,ED=3.求:(1)线段BD的长;
(2)∠AEC的正切值.
考点:解直角三角形
专题:计算题
分析:(1)利用同角的余角相等得到一对角相等,再由一对直角相等,得到三角形ABC与三角形DCE相似,由相似得比例,根据锐角三角函数定义及tan∠ACB的值,求出BC与CD的值,根据BC+CD求出BD的值即可;
(2)由三角形ABC与三角形DCE相似,根据AB与CD长求出相似比,进而求出AC与CE的比值,即为∠AEC的正切值.
(2)由三角形ABC与三角形DCE相似,根据AB与CD长求出相似比,进而求出AC与CE的比值,即为∠AEC的正切值.
解答:解:(1)∵∠ACE=90°,AB⊥BD,ED⊥BD,
∴∠ACB+∠ECD=90°,∠ACB+∠BAC=90°,∠B=∠D=90°,
∴∠BAC=∠ECD,
∴△ABC∽△CDE,
∴
=
,
∵tan∠ACB=
=2,AB=4,ED=3,
∴
=2,即BC=2,CD=6,
则BD=BC+CD=2+6=8;
(2)∵△ABC∽△CDE,
∴
=
=
=
,
则tan∠AEC=
=
.
∴∠ACB+∠ECD=90°,∠ACB+∠BAC=90°,∠B=∠D=90°,
∴∠BAC=∠ECD,
∴△ABC∽△CDE,
∴
| AB |
| BC |
| CD |
| ED |
∵tan∠ACB=
| AB |
| BC |
∴
| CD |
| ED |
则BD=BC+CD=2+6=8;
(2)∵△ABC∽△CDE,
∴
| AC |
| CE |
| AB |
| CD |
| 4 |
| 6 |
| 2 |
| 3 |
则tan∠AEC=
| AC |
| CE |
| 2 |
| 3 |
点评:此题属于解直角三角形题型,涉及的知识有:锐角三角函数定义,相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
下列调查中,适合用抽样调查的是( )
| A、了解报考军事院校考生的视力 |
| B、旅客上飞机前的安检 |
| C、对招聘教师中的应聘人员进行面试 |
| D、了解全市中小学生每天的零花钱 |
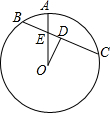 如图,D是⊙O弦BC的中点,A是
如图,D是⊙O弦BC的中点,A是
 如图,为测量一座地标性高楼的高度,小明在A点处测得楼顶D点的仰角为60°,在B点处测得楼顶D点的仰角为30°,A、B、C三点在一条直线上,已知AB=40
如图,为测量一座地标性高楼的高度,小明在A点处测得楼顶D点的仰角为60°,在B点处测得楼顶D点的仰角为30°,A、B、C三点在一条直线上,已知AB=40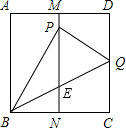 如图,有一边长为2的正方形ABCD,M,N分别是AD,BC边上的中点,将点C折到MN上,落在点P位置,折痕为BQ,连接PQ.求MP的长.
如图,有一边长为2的正方形ABCD,M,N分别是AD,BC边上的中点,将点C折到MN上,落在点P位置,折痕为BQ,连接PQ.求MP的长. 热气球的探测器显示,从热气球A看一栋高楼顶部B处的仰角为30°,看这栋高楼底部C处的俯角为60°,若热气球与高楼的水平距离为90m,则这栋高楼有多高?(结果保留整数,
热气球的探测器显示,从热气球A看一栋高楼顶部B处的仰角为30°,看这栋高楼底部C处的俯角为60°,若热气球与高楼的水平距离为90m,则这栋高楼有多高?(结果保留整数,