题目内容
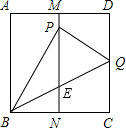如图，有一边长为2的正方形ABCD，M，N分别是AD，BC边上的中点，将点C折到MN上，落在点P位置，折痕为BQ，连接PQ．求MP的长．考点：翻折变换（折叠问题）,正方形的性质
专题：
分析：由中点的定义可得BN=1，折叠的性质可得BP=BC=2，在Rt△BPN中，根据勾股定理求PN的值，即可求得MP．
解答：解：∵ABCD是正方形，M、N分别为AD、BC的中点，
∴ABNM是矩形，BN=
BC=1，
∵BP=BC=1（折叠的性质），
在Rt△BPN中，
PN=
=
，
∴MP=MN-PN=2-
．
∴ABNM是矩形，BN=
| 1 |
| 2 |
∵BP=BC=1（折叠的性质），
在Rt△BPN中，
PN=
| 22-12 |
| 3 |
∴MP=MN-PN=2-
| 3 |
点评：此题主要考查折叠的性质，综合利用了正方形的性质、勾股定理、中点的定义等知识点．
练习册系列答案
阅读快车系列答案
相关题目
某班有50人，其中三好学生10人，优秀学生干部5人，在统计图上表示，能清楚地看出各部分与总数之间的百分比关系的是（ ）
| A、条形统计图 |
| B、扇形统计图 |
| C、折线统计图 |
| D、以上均可以 |
已知，如图，AC∥DE，AC=DE，BE=CF，求证：∠B=∠F．
某小区改造项目中，要将一棵没有价值的树放倒，栽上白玉兰，在操作过程中，李师傅要直接把树放倒，张师傅不同意，他担心这样会损坏这棵树周围7米处的花园和雕塑．请你根据图中标注的测量数据：∠BCD=60°，∠DCA=5°，BD=6米，通过计算说明：张师傅的担心是否有必要？（供选数据：sin65°≈0.9，cos65°≈0.4，tan65°≈2.1，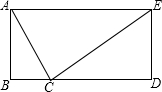
已知：如图，C是线段BD上一点，AB⊥BD，ED⊥BD，∠ACE=90°，tan∠ACB=2，AB=4，ED=3．求：