题目内容
 如图,已知二次函数y1=-
如图,已知二次函数y1=-| 1 |
| 2 |
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连结BA,BC,求△ABC的面积;
(3)求点B和点C所在直线的解析式y2,并根据图象求出当x为何值时,y1<y2.
考点:抛物线与x轴的交点,待定系数法求二次函数解析式,二次函数与不等式(组)
专题:
分析:(1)由二次函数y1=-
x2+bx+c的图象过A(2,0),B(0,-6)两点,直接利用待定系数法,即可求得这个二次函数的解析式;
(2)首先求得点C的坐标,继而求得△ABC的面积;
(3)首先求得直线BC的解析式,然后联立,可求得交点坐标,继而求得答案.
| 1 |
| 2 |
(2)首先求得点C的坐标,继而求得△ABC的面积;
(3)首先求得直线BC的解析式,然后联立,可求得交点坐标,继而求得答案.
解答:解:(1)∵二次函数y1=-
x2+bx+c的图象过A(2,0),B(0,-6)两点,
∴
,
解得:
,
∴这个二次函数的解析式为:y1=-
x2+4x-6;
(2)抛物线的对称轴为:x=-
=4,
∴C(4,0),
∴AC=4-2=2,
∴S△ABC=
AC•OB=
×2×6=6;
(3)设y2=mx+n,
∴
,
∴
,
∴y2=
x-6,
联立:
,
解得:
或
,
∴当x<0或x>5时,y1<y2.
| 1 |
| 2 |
∴
|
解得:
|
∴这个二次函数的解析式为:y1=-
| 1 |
| 2 |
(2)抛物线的对称轴为:x=-
| b |
| 2a |
∴C(4,0),
∴AC=4-2=2,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
(3)设y2=mx+n,
∴
|
∴
|
∴y2=
| 3 |
| 2 |
联立:
|
解得:
|
|
∴当x<0或x>5时,y1<y2.
点评:此题考查了二次函数与x轴的交点问题以及待定系数法求函数的解析式.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知方程组
的解是正数,则m的取值范围是( )
|
A、
| ||
B、-
| ||
C、-2<m<
| ||
D、-2<m≤
|
 如图,AB∥CD,FE平分∠GFD,GF与AB交于H,∠GHA=40°,那么∠BEF的度数是
如图,AB∥CD,FE平分∠GFD,GF与AB交于H,∠GHA=40°,那么∠BEF的度数是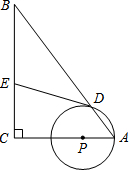 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,P为边AC上一个点(可以包括点C但不包括点A),以P为圆心PA为半径作⊙P交AB于点D,过点D作⊙P的切线交边BC于点E.试猜想BE与DE的数量关系,并说明理由.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,P为边AC上一个点(可以包括点C但不包括点A),以P为圆心PA为半径作⊙P交AB于点D,过点D作⊙P的切线交边BC于点E.试猜想BE与DE的数量关系,并说明理由.