题目内容
5.解不等式组:$\left\{\begin{array}{l}{9x+5<8x+7}\\{\frac{4}{3}x+2>1-\frac{2}{3}x}\end{array}\right.$并在数轴上标出不等式组的解的范围.分析 首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
解答 解:$\left\{\begin{array}{l}{9x+5<8x+7…①}\\{\frac{4}{3}x+2>1-\frac{2}{3}x…②}\end{array}\right.$,
解①得:x<2,
解②得:x>-$\frac{1}{2}$.
不等式组的解集是:-$\frac{1}{2}$<x<2.
点评 本题考查了不等式组的解法,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
相关题目
16.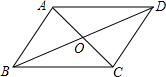 如图,?ABCD的对角线AC,BD相交于点O,下列条件可使的?ABCD为菱形的是( )
如图,?ABCD的对角线AC,BD相交于点O,下列条件可使的?ABCD为菱形的是( )
 如图,?ABCD的对角线AC,BD相交于点O,下列条件可使的?ABCD为菱形的是( )
如图,?ABCD的对角线AC,BD相交于点O,下列条件可使的?ABCD为菱形的是( )| A. | AC=BD | B. | ∠DAB=∠DCB | C. | AD=BC | D. | ∠AOD=90° |
20.已知直角三角形的两条直角边的长分别为$\sqrt{3}$和$\sqrt{6}$,则这个直角三角形的面积为( )
| A. | $\sqrt{18}$ | B. | 2$\sqrt{18}$ | C. | $\frac{3}{2}$$\sqrt{2}$ | D. | 18 |
10. 如图,直线AB、CD、EF交于点O,则图中与∠AOC互为对顶角的是( )
如图,直线AB、CD、EF交于点O,则图中与∠AOC互为对顶角的是( )
 如图,直线AB、CD、EF交于点O,则图中与∠AOC互为对顶角的是( )
如图,直线AB、CD、EF交于点O,则图中与∠AOC互为对顶角的是( )| A. | ∠BOE | B. | ∠BOD | C. | ∠DOE | D. | ∠BOC |
17.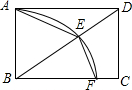 如图,在矩形ABCD中,以点B为圆心,AB长为半径画弧,交对角线BD于点E,交BC于点F,连接AE,EF.若∠BEF=70°,则∠DAE的度数是( )
如图,在矩形ABCD中,以点B为圆心,AB长为半径画弧,交对角线BD于点E,交BC于点F,连接AE,EF.若∠BEF=70°,则∠DAE的度数是( )
 如图,在矩形ABCD中,以点B为圆心,AB长为半径画弧,交对角线BD于点E,交BC于点F,连接AE,EF.若∠BEF=70°,则∠DAE的度数是( )
如图,在矩形ABCD中,以点B为圆心,AB长为半径画弧,交对角线BD于点E,交BC于点F,连接AE,EF.若∠BEF=70°,则∠DAE的度数是( )| A. | 10° | B. | 20° | C. | 25° | D. | 30° |
 抛物线y=ax2+bx+c(a≠0)与x轴交于A(2,0),B(4,0)两点,与y轴交于点C(0,2).
抛物线y=ax2+bx+c(a≠0)与x轴交于A(2,0),B(4,0)两点,与y轴交于点C(0,2).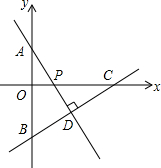 如图,在平面直角坐标系中,已知A,B两点的坐标分别是(0,2),0,-3),点P是x轴正半轴上一个动点,过点B作直线BC⊥AP于点D,直线BC与x轴交于点C.
如图,在平面直角坐标系中,已知A,B两点的坐标分别是(0,2),0,-3),点P是x轴正半轴上一个动点,过点B作直线BC⊥AP于点D,直线BC与x轴交于点C.