题目内容
18. 如图,AD⊥CD,AB=13,BC=12,CD=4,AD=3,∠CAB=α,求∠B.(用α表示)
如图,AD⊥CD,AB=13,BC=12,CD=4,AD=3,∠CAB=α,求∠B.(用α表示)
分析 根据勾股定理求出AC的长,根据勾股定理的逆定理判定△ABC是直角三角形,根据直角三角形的性质计算即可.
解答 解:∵AD⊥CD,CD=4,AD=3,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=5,
∵AC2+BC2=169,AB2=169,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,
∴∠B=90°-α.
点评 本题考查的是勾股定理和勾股定理的逆定理的应用,直角三角形中,两条直角边长的平方之和一定等于斜边长的平方;如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 如图,正方形网络中小方格的边长为1,A、B、C都是格点.
如图,正方形网络中小方格的边长为1,A、B、C都是格点.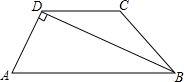 如图,等腰梯形ABCD,AB∥DC,AB=2,∠ADB=90°.
如图,等腰梯形ABCD,AB∥DC,AB=2,∠ADB=90°.