题目内容
 如图,已知AB∥CD,AE,DF分别是∠BAD,∠CDA的角平分线,求证:AE∥DF.
如图,已知AB∥CD,AE,DF分别是∠BAD,∠CDA的角平分线,求证:AE∥DF.考点:平行线的判定与性质
专题:证明题
分析:根据角平分线定义得出∠EAD=
∠BAD,∠FDA=
∠CDA,根据平行线的性质得出∠BAD=∠CDA,求出∠EAD=∠FDA,根据平行线的判定得出即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵AE,DF分别是∠BAD,∠CDA的角平分线,
∴∠EAD=
∠BAD,∠FDA=
∠CDA,
∵AB∥CD,
∴∠BAD=∠CDA,
∴∠EAD=∠FDA,
∴AE∥DE.
∴∠EAD=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB∥CD,
∴∠BAD=∠CDA,
∴∠EAD=∠FDA,
∴AE∥DE.
点评:本题考查了角平分线定义,平行线的性质和判定的应用,主要考查学生的推理能力.

练习册系列答案
相关题目
-(
)2的倒数是( )
| 1 |
| 2 |
| A、4 | ||
B、-
| ||
C、
| ||
| D、-4 |
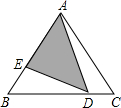 如图,△ABC的面积为1cm2,BD=2CD,AE=2BE,求阴影部分的面积.
如图,△ABC的面积为1cm2,BD=2CD,AE=2BE,求阴影部分的面积.