题目内容
 如图,过反比例函数y=
如图,过反比例函数y=| k |
| x |
| 6 |
| x |
考点:反比例函数系数k的几何意义
专题:探究型
分析:先根据反比例函数系数k的几何意义得出△AOC与△BOC的面积,再根据△ABO的面积为4即可求出k的值.
解答:解:∵AC⊥x轴,
∴S△AOC=
,S△BOC=
=3,
∵反比例函数y=
的图象在第一象限,
∴k>0,
∴S△AOC=
,
∵S△ABO=S△AOC-S△BOC=
-3=4,解得k=14.
故答案为:14.
∴S△AOC=
| |k| |
| 2 |
| 6 |
| 2 |
∵反比例函数y=
| k |
| x |
∴k>0,
∴S△AOC=
| k |
| 2 |
∵S△ABO=S△AOC-S△BOC=
| k |
| 2 |
故答案为:14.
点评:本题考查的是反比例函数系数k的几何意义,即在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是
,且保持不变.
| |k| |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
要使式子
有意义,则x的取值范围是( )
| x | ||
|
| A、x≥-3且x≠0 |
| B、.x≥-3 |
| C、x>-3 |
| D、全体实数 |
直线y=kx+k和双曲线y=
在同一坐标系中图象大致正确的是( )
| k |
| x |
A、 |
B、 |
C、 |
D、 |
已知|a|=5,|b|=3,且|a-b|=b-a,那么a+b的值为( )
| A、2 | B、-8 |
| C、-2或-8 | D、2或-8 |
 如图,E、F是平行四边形ABCD对角线AC上的两点,且BE∥DF.求证:∠1=∠2.
如图,E、F是平行四边形ABCD对角线AC上的两点,且BE∥DF.求证:∠1=∠2.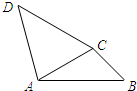 如图,在四边形ABCD中,∠ACB=∠BAD=105°,∠ABC=∠ADC=45°,若AB=2,则CD的长为
如图,在四边形ABCD中,∠ACB=∠BAD=105°,∠ABC=∠ADC=45°,若AB=2,则CD的长为