题目内容
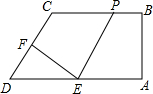
13．
如图，在四边形ABCD中，AB=CE，BE=CD，AB⊥BC于点B，DC⊥BC于点C，请判断AE和DE的数量关系及位置关系，并说明理由．
分析 根据已知条件可证得△ABE≌△ECD，由全等三角形的性质可知AE=DE，∠AEB=∠EDC，而∠EDC+∠DEC=90°，所以∠AEB+∠DEC=90°即AE⊥DE．
解答 解：AE=DE且AE⊥DE，
∵AB⊥BC，DC⊥BC，
∴∠B=∠C=90°，
在RT△ABE和RT△ECD中，
∵$\left\{\begin{array}{l}{AB=EC}\\{∠B=∠C=90°}\\{BE=CD}\end{array}\right.$，
∴△ABE≌△ECD（SAS），
∴AE=DE，∠AEB=∠EDC，
∵∠EDC+∠DEC=90°，
∴∠AEB+∠DEC=90°，
∴∠AED=90°，即AE⊥DE，
故AE=DE且AE⊥DE．
点评 本题主要考查全等三角形的判定和性质，本题求证△ABE≌△ECD是基础，利用互余、互补性质是关键．
练习册系列答案
相关题目
10．
请你用学习“一次函数”时积累的经验和方法解决下列问题：
（1）在平面直角坐标系中，画出函数y=|x|的图象：
①列表填空：
②描点、连线，画出y=|x|的图象；
（2）结合所画函数图象，写出y=|x|两条不同类型的性质；
（3）写出函数y=|x|与y=|x+2|图象的平移关系．
请你用学习“一次函数”时积累的经验和方法解决下列问题：（1）在平面直角坐标系中，画出函数y=|x|的图象：
①列表填空：
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | … |
（2）结合所画函数图象，写出y=|x|两条不同类型的性质；
（3）写出函数y=|x|与y=|x+2|图象的平移关系．
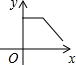
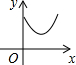
如图，在四边形ABCD中，BC∥AD，∠A=90°，BC＜AD，E为AD的中点，F为CD的中点，P是一动点，从点A开始沿AB-BC匀速运动，到达点C即止，记点P运动的时间为x，四边形PEFC的面积为y，y与x关系所反映的图象可能是（ ）
如图，△ACB为等腰直角三角形，∠ACB=90°，AC=BC，AE平分∠BAC，∠CDA=45°．求证：AD⊥BD．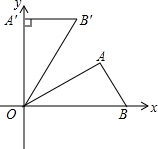
如图，在平面直角坐标系中，Rt△OAB的斜边OB在x轴的正半轴上，点A在第一象限，将△OAB，使点O按逆时针方向旋转至△OA′B′，使点A的对应点A′落在y轴的正半轴上，已知OB=2，∠AOB=30°．
3．如果a2-ab-4c是一个完全平方式，那么c等于（ ）
| A． | $\frac{1}{4}$b2 | B． | -$\frac{1}{8}$b2 | C． | $\frac{1}{16}$b2 | D． | -$\frac{1}{16}$b2 |