题目内容
5.(1)在函数$y=\sqrt{x+3}$中,自变量x的取值范围是x≥-3(2)已知y=$\sqrt{x-5}+\sqrt{5-x}-2$,则xy的值为$\frac{1}{25}$.
分析 (1)根据二次根式的有意义的条件列出不等式,解不等式即可;
(2)根据二次根式的有意义的条件列出不等式求出x、y的值,根据负整数指数幂的运算法则得到答案.
解答 解:(1)由题意得,x+3≥0,
解得x≥-3;
(2)由题意得,x-5≥0,5-x≥0,
解得,x=5,
则y=-2,
xy=$\frac{1}{25}$.
故答案为:(1)x≥-3;(2)$\frac{1}{25}$.
点评 本题考查的是二次根式有意义的条件,掌握二次根式中的被开方数必须是非负数是解题的关键.

练习册系列答案
相关题目
15.已知:关于x的方程x2+(1-2t)x+t2=0
(1)若方程有两个相等的实数根,求t的值;
(2)是否存在t,使方程的两个实数根的平方和等于7?若存在,请求出满足条件的t值;若不存在,请说明理由.
(1)若方程有两个相等的实数根,求t的值;
(2)是否存在t,使方程的两个实数根的平方和等于7?若存在,请求出满足条件的t值;若不存在,请说明理由.
16.任意三角形两边中点的连线与第三边上的中线( )
| A. | 互相平分 | B. | 互相垂直 | C. | 相等 | D. | 互相垂直平分 |
13.直角三角形两条边的长分别为:3,4,则第三边的长为( )
| A. | 5 | B. | $\sqrt{7}$ | C. | 7 | D. | 5或$\sqrt{7}$ |
10.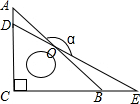 把一副三角板按如图放置,若∠A=45°,∠E=30°,则两条斜边相交所成的钝角∠AOE的度数为( )
把一副三角板按如图放置,若∠A=45°,∠E=30°,则两条斜边相交所成的钝角∠AOE的度数为( )
 把一副三角板按如图放置,若∠A=45°,∠E=30°,则两条斜边相交所成的钝角∠AOE的度数为( )
把一副三角板按如图放置,若∠A=45°,∠E=30°,则两条斜边相交所成的钝角∠AOE的度数为( )| A. | 165° | B. | 135° | C. | 115° | D. | 95° |
14.一个数的平方根和它的立方根相等,则这个数是( )
| A. | 1 | B. | 0 | C. | 1或0 | D. | 1或0或-1 |
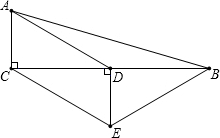 如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.求证:AD=BE.
如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.求证:AD=BE. 已知:如图,CD=AB且CD∥AB,E、F是直线AC上两点,且AE=CF.求证:
已知:如图,CD=AB且CD∥AB,E、F是直线AC上两点,且AE=CF.求证: