Question

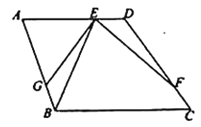
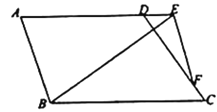
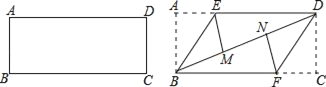
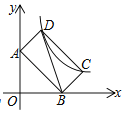
【题目】如图，矩形ABCD的边AB的解析式为y＝ax+2，顶点C，D在双曲线y＝（k＞0）上．若AB＝2AD，则k＝_____．

Answer 1

【答案】3

【解析】

过点D作DE⊥y轴于E，过点C作CF⊥x轴，根据直线的解析式求出点A、B的坐标，从而得到OA、OB．易证△AED∽△BOA，根据相似三角形的性质可求出ED、AE，从而可得到点D的坐标（用a表示），同理可得到点C的坐标（用a表示），然后根据点D、C在反比例函数的图象上得到关于a的方程，就可求得D的坐标，代入y＝（k＞0）即可求得．

过点D作DE⊥y轴于E，过点C作CF⊥x轴，如图所示．

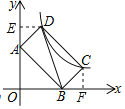
∵点A、B是直线y＝ax+2分别与y轴、x轴的交点，

∴A（0，2），B（﹣，0），

∴OA＝2，OB＝﹣．

∵四边形ABCD是矩形，

∴∠A＝90°，AD＝BC．

∵AB＝2AD，

∴，

∴．

∵∠DEA＝∠AOB＝90°，∠EAD＝∠ABO＝90°﹣∠OAB，

∴△AED∽△BOA，

∴＝＝＝，

∴ED＝1，AE＝﹣，

∴点D（1，2﹣）．

同理：点C（1﹣，﹣）．

∵点C、D都在反比例函数y＝（k＞0）的图象上，

∴1×（2﹣）＝（1﹣）（﹣），

∴a＝±1．

∵a＜0，

∴a＝﹣1，

∴点D的坐标为（1，3），

∴k＝1×3＝3，

故答案为3．