Question

【题目】已知四边形中，，，点是射线上一点，点是射线上一点，且满足.

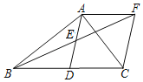
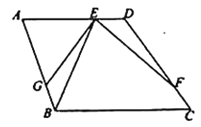
（1）如图，当点在线段上时，若，在线段上截取，联结.求证：；

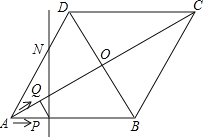
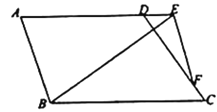
（2）如图，当点在线段的延长线上时，若，，，设，，求关于的函数关系式及其定义域；

（3）记与交于点，在（2）的条件下，若与相似，求线段的长.

Answer 1

【答案】（1）证明见详解；（2） ；（3） .

【解析】

(1)证明△EGB≌△FDE，根据全等三角形的性质即可证明.

(2) H为BC上一点，使四边形ABHD为等腰梯形，连接DH，作BI⊥AD于点I，作HJ⊥AD于点J,作DK⊥BC于点K，根据∠A=∠ADH=∠DHC，∠ABC=∠BHD=∠HDC+∠C∠ABC=2∠C，得到∠HDC=∠C，由,得到HD=HC=AB=3,AI=DJ=HK=1,

则，求出 作∠ENF=∠A，证明△DFN∽△DHC，又△NEF∽△ABE，根据相似三角形的性质得到

DE=x-4，代入,即可求出关于的函数关系式及其定义域；

(3) 根据△EMF∽△EMF，得到∠AEB=∠EFM=∠EFN，则∠AEB=∠EDC=∠C，

在AE上截取PE=BP，∠AEB=∠PBE=∠APB，证明△APB∽△HDC,根据相似三角形的性质得到△ABP的三边比为，即可求出BP=PE=，即可求出线段的长.

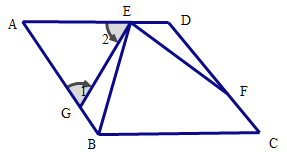
(1)证明：∵AD∥BC

∴∠A+∠ABC=180°,∠ADC+∠C=180°，

又∵∠A+∠1+∠2=180°，

又∵∠1=∠2

∴∠ABC=2∠1.

且∠ABC=2∠C，∴∠C=∠1，

∵∠BGE+∠1=180°

∴∠ADC=∠BGE，

∵∠A+∠ABE+∠AEB=180°，∠AEB+∠BEF+∠DEF=180°，

且∠A=∠BEF

∴∠ABE=∠DEF

∵AB=AD,AG=AE

∴BG=DE

∴△EGB≌△FDE

∴GE=DF.

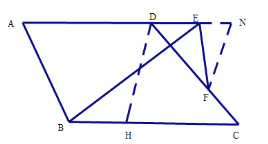
(2)H为BC上一点，使四边形ABHD为等腰梯形，连接DH，作BI⊥AD于点I，作HJ⊥AD于点J,作DK⊥BC于点K，

易得∠A=∠ADH=∠DHC，∠ABC=∠BHD=∠HDC+∠C

又∵∠ABC=2∠C，

∴∠HDC=∠C

∵ ,

∴HD=HC=AB=3,AI=DJ=HK=1,

∴

∴

作∠ENF=∠A，

∴∠DHC=∠A=∠ENF，

∵∠NDF=∠C,

∴△DFN∽△DHC，

又∵△NEF∽△ABE

∴

∴DE=x-4

∴

,

∴

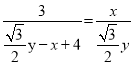
(3)∵△EMF与△ABE相似，

此时只有△EMF∽△EMF

∴∠AEB=∠EFM=∠EFN

∴∠AEB= ∠EDC= ∠C

解△ABE,在AE上截取PE=BP，

∴∠AEB=∠PBE=∠APB

∴∠APB=∠C

∴△APB∽△HDC,

∴△ABP的三边比为，

∴BP=PE=

∴AE=AP+PE=.