Question

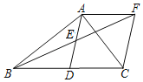
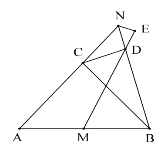
【题目】如图，△ABC 为等腰直角三角形，∠ACB＝90°，点 M 为 AB 边的中点，点 N 为射线 AC 上一点，连接 BN，过点 C 作 CD⊥BN 于点 D，连接 MD，作∠BNE＝∠BNA，边 EN 交射线 MD 于点 E，若 AB＝20，MD＝14，则 NE 的长为___.

Answer 1

【答案】

【解析】

连接CM，过点M作MF⊥BD于F，根据等腰直角三角形的性质求出BM、BC，证出C、M、B、D四点共圆，根据圆周角定理的推论和等腰三角形的判定证出△DMF为等腰直角三角形，利用勾股定理和锐角三角函数求出BD和BN，然后证出△NDE∽△MDB列出比例式即可求出结论．

解：连接CM，过点M作MF⊥BD于F

∵△ABC 为等腰直角三角形，∠ACB＝90°，点 M 为 AB 边的中点，AB＝20，

∴BM=AB=10，AC=BC=20，∠CMB=90°，∠BCM=∠ACB＝45°

∵CD⊥BN

∴∠CDB=90°

∴∠CDB＋∠CMB=180°

∴C、M、B、D四点共圆

∴∠MDB=∠BCM=45°，∠DCB=∠BMD

∴△DMF为等腰直角三角形

∵MD＝14，

∴MF=DF=14

在Rt△BMF中，BF=

∴BD=BF＋DF=16

∵cos∠CBN=

即

解得：BN=25

∴DN=BN－BD=9

∵∠BNE＝∠BNA，而∠DCN＋∠BNA=90°

∴∠BNE＋∠DCN=90°

∵∠DCN＋∠DCB=90°

∴∠BNE=∠DCB

∴∠BNE=∠BMD

∵∠NDE=∠MDB

∴△NDE∽△MDB

∴

即

解得：NE=

故答案为：．