题目内容
14.关于抛物线y=x2-4x-5,下列结论不正确的是( )| A. | 抛物线开口向上 | B. | 抛物线的对称轴是x=2 | ||
| C. | 当x=2时,y的最大值为-9 | D. | 抛物线与x轴的交点为(-1,0),(5,0) |
分析 根据二次函数的性质确定其开口方向、对称轴、最值及与坐标轴的交点坐标后即可确定正确的选项.
解答 解:∵y=x2-4x-5中,a=1>0,
∴开口向上,A答案正确,不符合题意;
∵y=x2-4x-5=(x-2)2-9,
∴对称轴为x=2,B答案正确,不符合题意;
当x=2时有最小值-9,C答案错误,符合题意;
∵当y=x2-4x-5=0时,
解得:x=-1或x=5,
∴抛物线与x轴的交点为(-1,0),(5,0)正确,不符合题意,
故选C.
点评 本题考查了抛物线的性质与解析式的关系.关键是明确抛物线解析式各项系数与性质的联系.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
2.点M(4,-3)关于y轴对称的点N的坐标是( )
| A. | (4,3) | B. | (4,-3) | C. | (-4,3) | D. | (-4,-3) |
19.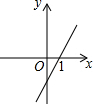 已知一次函数y=kx+b的图象如图所示,则下列语句中不正确的是( )
已知一次函数y=kx+b的图象如图所示,则下列语句中不正确的是( )
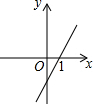 已知一次函数y=kx+b的图象如图所示,则下列语句中不正确的是( )
已知一次函数y=kx+b的图象如图所示,则下列语句中不正确的是( )| A. | 函数值y随x的增大而增大 | B. | 当x>0时,y>0 | ||
| C. | k+b=0 | D. | kb<0 |
6.在平面直角坐标系中,点P(-3,7)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
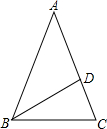 如图,在△ABC中,AB=AC,∠A=36°,点D是AC上一点,BD平分∠ABC.
如图,在△ABC中,AB=AC,∠A=36°,点D是AC上一点,BD平分∠ABC.