Question

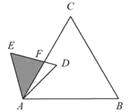
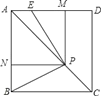
【题目】如图，已知正方形ABCD的边长为1，P是对角线AC上任意一点，E为AD上的点，且∠EPB=90°，PM⊥AD，PN⊥AB．

（1）求证：四边形PMAN是正方形；

（2）求证：EM=BN；

（3）若点P在线段AC上移动，其他不变，设PC=x，AE=y，求y关于x的解析式，并写出自变量x的取值范围．

Answer 1

【答案】（1）见解析；（2）见解析；（3）y=1-（0≤x≤）.

【解析】

（1）由四边形ABCD是正方形，易得∠BAD=90°，AC平分∠BAD，又由PM⊥AD，PN⊥AB，即可证得四边形PMAN是正方形；
（2）由四边形PMAN是正方形，易证得△EPM≌△BPN，即可证得：EM=BN；
（3）首先过P作PF⊥BC于F，易得△PCF是等腰直角三角形，继而证得△APM是等腰直角三角形，可得AP=AM=（AE+EM），继而求得答案．

（1）.∵正方形ABCD，

∴∠NAM=90.

又因为PM⊥AD,PN⊥AB，

∴∠ANP=∠AMP=90，

∴四边形PMAN是矩形（有三个角是直角）.

∵P在AC上，

∴PM=PN（角平分线上的点到这条线段两边的距离相等），

∴四边形PMAN是正方形；

（2）.∵∠EPB=90，

∴∠BPN+∠APN=90.

∵∠EPM=∠APN=90，

∴∠BPN=∠EPM，

在△BPN与△EPM中

∠BPN=∠EPM，PN=PM，∠BNP=∠EMP，

∴△BPN≌△EPM，

∴BN=EM；

（3）过P作PF⊥BC于F，如图所示：

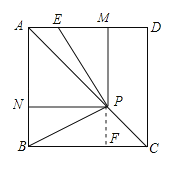
∵四边形ABCD是正方形，

∴∠ABC=90°，AB=BC=1，∠PCF=45°，

∴AC=，△PCF是等腰直角三角形，

∴AP=AC-PC=-x，BN=PF=，

∴EM=BN=，

∵∠PAM=45°，∠PMA=90°，

∴△APM是等腰直角三角形，

∴AP=AM=（AE+EM），

即-x=（y+），

解得：y=1-x，

∴x的取值范围为0≤x≤，

∴y=1-x（0≤x≤）．