题目内容
17.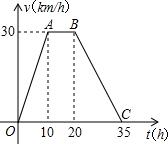 据某气象站观察和预测:发生于A地的热带风暴正向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示.
据某气象站观察和预测:发生于A地的热带风暴正向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示.(1)试求v(km/h)与时间t(h)的函数解析式;
(2)过线段OC上一点T(t,0)作横轴的垂线1,据物理学知识可以得到:梯形OABC在直线1左侧部分的面积为t(h)内热带风暴所经过的路程s(km).
①试求s(km)与时间t(h)的函数解析式;
②若M,N两城分别位于A地正南方向,且距A地为700km和600km,试判断这场热带风暴是否会侵袭到M,N两城?如果会,在热带风暴发生后多长时间它将侵袭到M,N两城?如果不会,请说明理由(结果精确到1h,$\sqrt{5}$≈2.2)
分析 (1)先求出点C的坐标即可得出直线OA的解析式,再求出点B,C坐标即可求出直线BC的解析式;
(2)①分三种情况,利用面积的和差即可得出结论;
②先判断M,N两城是否受到侵袭,然后求出沙尘暴过后30h受到侵袭.
解答 解:(1)当0≤t≤10时,∵A的坐标分别为(10,30),
∴直线OA的解析式为v=3t,
当10<t≤20时,直线AB的解析式为v=30,
当20<t≤35时,
∵B,C的坐标分别为(20,30),(35,0)
∴直线BC的解析式为v=-2t+70,
(2)①设直线l交v与t的函数图象于D点,
当0≤t≤10时,此时OT=t,TD=3t(如图1),
∴S=$\frac{1}{2}•t•3t$=$\frac{3}{2}$t2,
当10<t≤20时,此时OT=t,AD=ET=t-10,TD=30(如图2)
∴S=S△AOE+S矩形ADTE=$\frac{1}{2}$×10×30+30(t-10)=30t-150
当20<t≤35时,
∵B,C的坐标分别为(20,30),(35,0)
∴直线BC的解析式为v=-2t+70
∴D点坐标为(t,-2t+70),
∴TC=35-t,TD=-2t+70(如图3)
∴S=S四边形OABC-S△DCT=$\frac{1}{2}$(10+35)×30-$\frac{1}{2}$(35-t)(-2t+70)=-(35-t)2+675
②∵当t=20时,S=30×20-150=450(km),
当t=35时,S=-(35-35)2+675=675(km),
∵700(km)>675(km),
∴M城不会受到侵袭,
又∵450<650<675,
∴N城会受到侵袭,且侵袭时间t应在20h至35h之间,
由-(35-t)2+675=650,解得t=30或t=40(不合题意,舍去).
所以在沙尘暴发生后30h它将侵袭到N城.
点评 此题是四边形综合题,主要考查了待定系数法,几何图形的面积的计算方法,分类讨论的思想,解本题的关键是用分类讨论的思想解决问题.

| 选 手 | 甲 | 乙 | 丙 | 丁 |
| 方差(环2) | 0.35 | 0.018 | 0.22 | 0.055 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
 如图,四边形ABCD是平行四边形,对角线AC,BD交于点O,且△OAB为等边三角形.求证:四边形ABCD为矩形.
如图,四边形ABCD是平行四边形,对角线AC,BD交于点O,且△OAB为等边三角形.求证:四边形ABCD为矩形.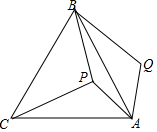 如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,若PA=6,PB=8,PC=10,则∠APB=150°.
如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,若PA=6,PB=8,PC=10,则∠APB=150°. 如图,矩形ABCD中,AB=8,AD=12,E为AD中点,F为CD边上任意一点,G,H分别为EF,BF中点,求GH的长.
如图,矩形ABCD中,AB=8,AD=12,E为AD中点,F为CD边上任意一点,G,H分别为EF,BF中点,求GH的长.