题目内容
2．
如图，矩形ABCD中，AB=8，AD=12，E为AD中点，F为CD边上任意一点，G，H分别为EF，BF中点，求GH的长．
分析 连接BE．根据中点的定义求得AE=6．根据矩形的性质和勾股定理可求BE，再根据三角形中位线定理可求GH的长．
解答 
解：连接BE．
∵E为AD中点，AD=12，
∴AE=6．
∵四边形ABCD是矩形，
∴∠A=90°．
在Rt△ABE中，AB=8，依据勾股定理BE2=AB2+AE2，
∴BE=10．
∵G，H分别为EF，BF中点，
∴GH=$\frac{1}{2}$BE=5．
点评 本题考查了矩形的性质，勾股定理，三角形中位线定理，正确的添加辅助线是解题的关键．
练习册系列答案
相关题目
线段CD是由线段AB平移得到的，点A（-1，0）的对应点为C（1，-1），则点B（0，3）的对应点D的坐标是（2，2）．
10．
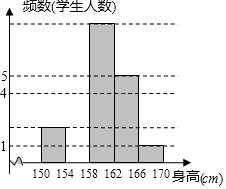下面数据是20位同学的身高（单位：cm）：
156 154 161 158 164 150 163 160 159 155
159 161 157 168 163 159 165 164 158 153
（1）这组数据中，最大值与最小值的差是18；
（2）将这组数据分为5组：150≤x＜154，154≤x＜158，158≤x＜162，162≤x＜166，166≤x＜170，则组距是4；
（3）完成下面频数分布表，并将频数分布直方图补充完整．
下面数据是20位同学的身高（单位：cm）：156 154 161 158 164 150 163 160 159 155
159 161 157 168 163 159 165 164 158 153
（1）这组数据中，最大值与最小值的差是18；
（2）将这组数据分为5组：150≤x＜154，154≤x＜158，158≤x＜162，162≤x＜166，166≤x＜170，则组距是4；
（3）完成下面频数分布表，并将频数分布直方图补充完整．
| 身高分组 | 划记 | 频数 |
| 150≤x＜154 | ||
| 154≤x＜158 | ||
| 158≤x＜162 | ||
| 162≤x＜166 | 正 | 5 |
| 166≤x＜170 | ￣ | 1 |
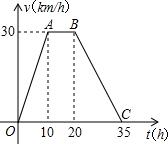据某气象站观察和预测：发生于A地的热带风暴正向正南方向移动，其移动速度v（km/h）与时间t（h）的函数图象如图所示．
如图，等边△ABC的边长是2，D、E分别为AB、AC的中点，延长BC至点F，使CF=$\frac{1}{2}$BC，连接CD和EF．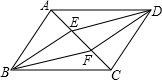
如图，四边形ABCD是平行四边形，且DE∥BF，分别交对角线AC于点E、F，连接EB，FD．