题目内容
14.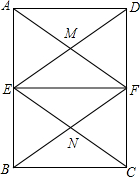 如图.点E、F分别是矩形ABCD的两条长边AB、CD的中点.AF与DE相交于点M.CE与BF相交于点N.
如图.点E、F分别是矩形ABCD的两条长边AB、CD的中点.AF与DE相交于点M.CE与BF相交于点N.(1)写出四条不同类型的结论.
(2)连接MN.若MN=AM.求证:△AEM是等边三角形.
分析 (1)由矩形的性质和判定以及平行四边形的判定与性质即可得出结果;
(2)由矩形的性质得出AB=DC,AB∥DC,∠EAD=∠EBC=90°,证出AE=BE=DF=CF,得出四边形AEFD、四边形BEFC是平行四边形,得出四边形AEFD、四边形BEFC是矩形,得出AM=EM=FM,BN=FN,证出MN是△ABF的中位线,由三角形中位线定理得出MN=$\frac{1}{2}$AB=AE,证出AM=AE=EM即可.
解答 (1)解:四边形AEFD是矩形,AM=EM,四边形BEDF是平行四边形,AF=EC;
(2)证明:如图所示: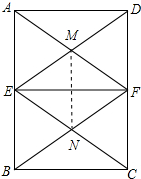
∵四边形ABCD是矩形,
∴AB=DC,AB∥DC,∠EAD=∠EBC=90°,
∵点E、F分别是矩形ABCD的两条长边AB、CD的中点,
∴AE=BE=DF=CF,
∴四边形AEFD、四边形BEFC是平行四边形,
又∵∠EAD=∠EBC=90°,
∴四边形AEFD、四边形BEFC是矩形,
∴AM=EM=FM,BN=FN,
∴△AEM是等腰三角形,MN是△ABF的中位线,
∴MN=$\frac{1}{2}$AB=AE,
∵MN=AM,
∴AM=AE=EM,
即△AEM是等边三角形.
点评 本题考查了矩形的性质与判定、平行四边形的判定与性质、三角形中位线定理、等边三角形的判定;熟练掌握矩形的性质,由三角形中位线定理得出MN等于AB的一半是解决问题的关键.

练习册系列答案
相关题目
2.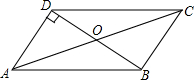 如图,在?ABCD中,∠ODA=90°,AC=20cm,BD=12cm,则AD的长为( )
如图,在?ABCD中,∠ODA=90°,AC=20cm,BD=12cm,则AD的长为( )
 如图,在?ABCD中,∠ODA=90°,AC=20cm,BD=12cm,则AD的长为( )
如图,在?ABCD中,∠ODA=90°,AC=20cm,BD=12cm,则AD的长为( )| A. | 8cm | B. | 10cm | C. | 12cm | D. | 16cm |
19.一元二次方程x2-3x+1=0的两根为x1、x2,则x1+x2=( )
| A. | 3 | B. | -3 | C. | 1 | D. | -1 |
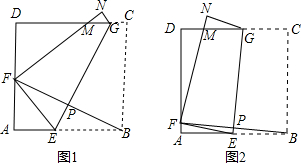
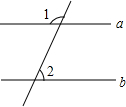 如图,a∥b,∠1=130°,则∠2=50°.
如图,a∥b,∠1=130°,则∠2=50°.