题目内容
13.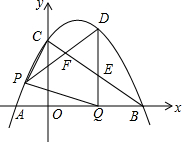 如图,抛物线y=-$\frac{\sqrt{3}}{9}$x2+$\frac{2\sqrt{3}}{3}$x+3$\sqrt{3}$与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).
如图,抛物线y=-$\frac{\sqrt{3}}{9}$x2+$\frac{2\sqrt{3}}{3}$x+3$\sqrt{3}$与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).(1)求直线BC的函数表达式;
(2)①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简)
②在点P、Q运动的过程中,当PQ=PD时,求t的值;
(3)试探究在点P,Q运动的过程中,是否存在某一时刻,使得点F为PD的中点?若存在,请直接写出此时t的值与点F的坐标;若不存在,请说明理由.
分析 (1)更好函数的解析式得到B(9,0),C(0,3$\sqrt{3}$),解方程组即可得到结论;
(2)①过p作PG⊥x轴于G,解直角三角形得到∠CAO=60°,得到PG=$\frac{\sqrt{3}}{2}$t,AG=$\frac{1}{2}$t,于是得到P($\frac{1}{2}$t-3,$\frac{\sqrt{3}}{2}$t),把OQ=9-2t代入二次函数的解析式即可得到D(9-2t,-$\frac{4\sqrt{3}}{9}$t2+$\frac{8\sqrt{3}}{3}$t),②过P作PH⊥QD于H,得到四边形PGQH是矩形,列方程即可得到即可;
(3)根据折叠坐标公式得到F(-$\frac{3}{4}$t+3,-$\frac{2\sqrt{3}}{9}$t2+$\frac{19}{12}$$\sqrt{3}$t),由点F在直线BC上,列方程即可得到结论.
解答  解:(1)由y=0得-$\frac{\sqrt{3}}{9}$x2+$\frac{2\sqrt{3}}{3}$x+3$\sqrt{3}$=0,
解:(1)由y=0得-$\frac{\sqrt{3}}{9}$x2+$\frac{2\sqrt{3}}{3}$x+3$\sqrt{3}$=0,
解得:x1=-3,x2=9,
∴B(9,0),
由x=0得y=3$\sqrt{3}$,
∴C(0,3$\sqrt{3}$),
设直线BC的解析式为y=kx+b,∴$\left\{\begin{array}{l}{9k+b=0}\\{b=3\sqrt{3}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=3\sqrt{3}}\end{array}\right.$,
∴直线BC的解析式为y=-$\frac{\sqrt{3}}{3}$x+3$\sqrt{3}$;
(2)①过P作PG⊥x轴于G,
∵A(-3,0),C(0,3$\sqrt{3}$),
∴OA=3.OC=3$\sqrt{3}$,
∴tan∠CAO=$\sqrt{3}$,
∴∠CAO=60°,
∵AP=t,
∴PG=$\frac{\sqrt{3}}{2}$t,AG=$\frac{1}{2}$t,
∴OG=3-$\frac{1}{2}$t,
∴P($\frac{1}{2}$t-3,$\frac{\sqrt{3}}{2}$t),
∵DQ⊥x轴,BQ=2t,
∴OQ=9-2t,
∴D(9-2t,-$\frac{4\sqrt{3}}{9}$t2+$\frac{8\sqrt{3}}{3}$t),
②过P作PH⊥QD于H,
则四边形PGQH是矩形,
∴HQ=PG,∵PQ=PD,PH⊥QD,∴DQ=2HQ=2PG,∵P($\frac{1}{2}$t-3,$\frac{\sqrt{3}}{2}$t),D(9-2t,-$\frac{4\sqrt{3}}{9}$t2+$\frac{8\sqrt{3}}{3}$t),
∴-$\frac{4\sqrt{3}}{9}$t2+$\frac{8\sqrt{3}}{3}$t=2×$\frac{\sqrt{3}}{2}$t,
解得:t1=0(舍去),t2=$\frac{15}{4}$,∴当PQ=PD时,t的值是$\frac{15}{4}$;
(3)∵点F为PD的中点,
∴F的横坐标为:$\frac{1}{2}$($\frac{1}{2}$t-3+9-2t)=-$\frac{3}{4}$t+3,F的纵坐标为$\frac{1}{2}$($\frac{\sqrt{3}}{2}$t-$\frac{4\sqrt{3}}{9}$t2+$\frac{8\sqrt{3}}{3}$t)=-$\frac{2\sqrt{3}}{9}$t2+$\frac{19}{12}$$\sqrt{3}$t,
∴F(-$\frac{3}{4}$t+3,-$\frac{2\sqrt{3}}{9}$t2+$\frac{19}{12}$$\sqrt{3}$t),
∵点F在直线BC上,
∴-$\frac{2\sqrt{3}}{9}$t2+$\frac{19}{12}$$\sqrt{3}$t=-$\frac{\sqrt{3}}{3}$(-$\frac{3}{4}$t+3)+3$\sqrt{3}$,
∴t=3,
∴F($\frac{3}{4}$,$\frac{11\sqrt{3}}{4}$).
点评 本题考查了待定系数法求函数解析式,解直角三角形,矩形的判定和性质,中点坐标公式,方程的解法,正确的作出辅助线是解题的关键.

| A. |  | B. |  | C. |  | D. |  |
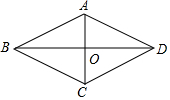 求证:菱形的两条对角线互相垂直.
求证:菱形的两条对角线互相垂直.已知:如图,四边形ABCD是菱形,对角线AC,BD交于点O.
求证:AC⊥BD.
以下是排乱的证明过程:
①又BO=DO;
②∴AO⊥BD,即AC⊥BD;
③∵四边形ABCD是菱形;
④∴AB=AD.
证明步骤正确的顺序是( )
| A. | ③→②→①→④ | B. | ③→④→①→② | C. | ①→②→④→③ | D. | ①→④→③→② |
 某商店经销一种品牌的洗衣机,其中某一型号的洗衣机每台进价为a元,商店将进价提高20%后作为零售价进行销售,一段时间后,商店又以9折优惠价促销,这时该型号洗衣机的零售价为1.08a元.
某商店经销一种品牌的洗衣机,其中某一型号的洗衣机每台进价为a元,商店将进价提高20%后作为零售价进行销售,一段时间后,商店又以9折优惠价促销,这时该型号洗衣机的零售价为1.08a元.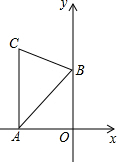 如图,AC⊥x轴于点A,点B在y轴的正半轴上,∠ABC=60°,AB=4,BC=2$\sqrt{3}$,点D为AC与反比例函数y=$\frac{k}{x}$的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为-4或-8.
如图,AC⊥x轴于点A,点B在y轴的正半轴上,∠ABC=60°,AB=4,BC=2$\sqrt{3}$,点D为AC与反比例函数y=$\frac{k}{x}$的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为-4或-8. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( )
“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( )