题目内容
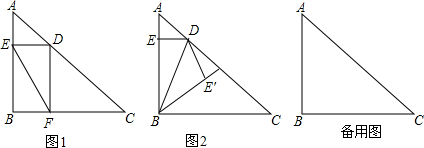
 小方与同学一起去郊游,看到一棵大树斜靠在一小土坡上,他想知道树有多长,于是他借来测角仪和卷尺.如图,他在点C处测得树AB顶端A的仰角为30°,沿着CB方向向大树行进10米到达点D,测得树AB顶端A的仰角为45°,又测得树AB倾斜角∠1=75°.
小方与同学一起去郊游,看到一棵大树斜靠在一小土坡上,他想知道树有多长,于是他借来测角仪和卷尺.如图,他在点C处测得树AB顶端A的仰角为30°,沿着CB方向向大树行进10米到达点D,测得树AB顶端A的仰角为45°,又测得树AB倾斜角∠1=75°.(1)求AD的长.
(2)求树长AB.
考点:解直角三角形的应用-仰角俯角问题
专题:几何图形问题
分析:(1)过点A作AE⊥CB于点E,设AE=x,分别表示出CE、DE,再由CD=10,可得方程,解出x的值,在Rt△ADE中可求出AD;
(2)过点B作BF⊥AC于点F,设BF=y,分别表示出CF、AF,解出y的值后,在Rt△ABF中可求出AB的长度.
(2)过点B作BF⊥AC于点F,设BF=y,分别表示出CF、AF,解出y的值后,在Rt△ABF中可求出AB的长度.
解答: 解:(1)过点A作AE⊥CB于点E,设AE=x,
解:(1)过点A作AE⊥CB于点E,设AE=x,
在Rt△ACE中,∠C=30°,
∴CE=
x,
在Rt△ADE中,∠ADE=45°,
∴DE=AE=x,
∴CE-DE=10,即
x-x=10,
解得:x=5(
+1),
∴AD=
x=5
+5
答:AD的长为(5
+5
)米.
(2)由(1)可得AC=2AE=(10
+10)米,
过点B作BF⊥AC于点F,
∵∠1=75°,∠C=30°,
∴∠CAB=45°,
设BF=y,
在Rt△CBF中,CF=
BF=
y,
在Rt△BFA中,AF=BF=y,
∴
y+y=(10
+10),
解得:y=10,
在Rt△ABF中,AB=
=10
米.
答:树高AB的长度为10
米.
 解:(1)过点A作AE⊥CB于点E,设AE=x,
解:(1)过点A作AE⊥CB于点E,设AE=x,在Rt△ACE中,∠C=30°,
∴CE=
| 3 |
在Rt△ADE中,∠ADE=45°,
∴DE=AE=x,
∴CE-DE=10,即
| 3 |
解得:x=5(
| 3 |
∴AD=
| 2 |
| 6 |
| 2 |
答:AD的长为(5
| 6 |
| 2 |
(2)由(1)可得AC=2AE=(10
| 3 |
过点B作BF⊥AC于点F,
∵∠1=75°,∠C=30°,
∴∠CAB=45°,
设BF=y,
在Rt△CBF中,CF=
| 3 |
| 3 |
在Rt△BFA中,AF=BF=y,
∴
| 3 |
| 3 |
解得:y=10,
在Rt△ABF中,AB=
| AF2+BF2 |
| 2 |
答:树高AB的长度为10
| 2 |
点评:本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用锐角三角函数及已知线段表示未知线段,有一定难度.

练习册系列答案
相关题目

 在平面内正方形ABCD与正方形CEFH如图放置,连DE,BH,两线交于M.求证:
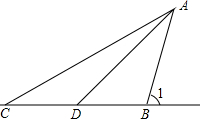
在平面内正方形ABCD与正方形CEFH如图放置,连DE,BH,两线交于M.求证: 如图,一堤坝的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到0.01米)
如图,一堤坝的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到0.01米)