题目内容
若实数m，n 满足|m-2|+（n-2014）2=0，则m-1+n0= ．
考点：负整数指数幂,非负数的性质：绝对值,非负数的性质：偶次方,零指数幂
专题：
分析：根据绝对值与平方的和为0，可得绝对值与平方同时为0，根据负整指数幂、非0的0次幂，可得答案．
解答：解：|m-2|+（n-2014）2=0，
m-2=0，n-2014=0，
m=2，n=2014．
m-1+n0=2-1+20140=
+1=
，
故答案为：
．
m-2=0，n-2014=0，
m=2，n=2014．
m-1+n0=2-1+20140=
| 1 |
| 2 |
| 3 |
| 2 |
故答案为：
| 3 |
| 2 |
点评：本题考查了负整指数幂，先求出m、n的值，再求出负整指数幂、0次幂．
练习册系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
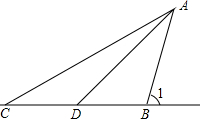小方与同学一起去郊游，看到一棵大树斜靠在一小土坡上，他想知道树有多长，于是他借来测角仪和卷尺．如图，他在点C处测得树AB顶端A的仰角为30°，沿着CB方向向大树行进10米到达点D，测得树AB顶端A的仰角为45°，又测得树AB倾斜角∠1=75°．
在△ABC中，分别以AB，AC为斜边作Rt△ABD和Rt△ACE，∠ADB=∠AEC=90°，∠ABD=∠ACE=30°，连接DE．若DE=5，则BC长为已知点P（1-2a，a-2）关于原点的对称点在第一象限内，且a为整数，则关于x的分式方程
=2的解是（ ）
| x+1 |
| x-a |
| A、5 | B、1 | C、3 | D、不能确定 |
