题目内容
13.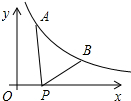 如图所示,已知A(1,y1),B(2,y2)为反比例函数y=$\frac{2}{x}$图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大值时,点P的坐标是( )
如图所示,已知A(1,y1),B(2,y2)为反比例函数y=$\frac{2}{x}$图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大值时,点P的坐标是( )| A. | (3,0) | B. | ($\frac{7}{2}$,0) | C. | ($\frac{5}{3}$,0) | D. | ($\frac{5}{2}$,0) |
分析 求出A、B的坐标,设直线AB的解析式是y=kx+b,把A、B的坐标代入求出直线AB的解析式,根据三角形的三边关系定理得出在△ABP中,|AP-BP|<AB,延长AB交x轴于P′,当P在P′点时,PA-PB=AB,此时线段AP与线段BP之差达到最大,求出直线AB于x轴的交点坐标即可.
解答 解:∵把A(1,y1),B(2,y2)代入反比例函数y=$\frac{2}{x}$得:y1=2,y2=1,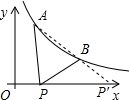
∴A(1,2),B(2,1),
∵在△ABP中,由三角形的三边关系定理得:|AP-BP|<AB,
∴延长AB交x轴于P′,当P在P′点时,PA-PB=AB,
即此时线段AP与线段BP之差达到最大,
设直线AB的解析式是y=kx+b,
把A、B的坐标代入得:$\left\{\begin{array}{l}{k+b=2}\\{2k+b=1}\end{array}\right.$,
解得:k=-1,b=3,
∴直线AB的解析式是y=-x+3,
当y=0时,x=3,
即P(3,0).
故选A.
点评 本题主要考查了反比例函数的综合题的知识,熟练掌握三角形的三边关系定理和用待定系数法求一次函数的解析式,解此题的关键是确定P点的位置,题目比较好,但有一定的难度.

练习册系列答案
相关题目
4.若将函数y=2x2的图象向右平行移动5个单位,再向上平移1个单位,可得到的抛物线是( )
| A. | y=2(x-5)2+1 | B. | y=2(x-5)2-1 | C. | y=2(x+5)2-1 | D. | y=2(x+5)2+1 |
1.为鼓励大学生创业,我市为在开发区创业的每位大学生提供无息贷款125000元,这个数据用科学记数法表示为(保留两位有效数字)( )
| A. | 1.2×105 | B. | 1.2×105 | C. | 1.3×105 | D. | 1.3×106 |
2.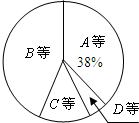 某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
(1)试直接写出x、y的值;
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?
 某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.| 等第 | 成绩(得分) | 频数(人数) | 频率 |
| A | 10分 | 7 | 0.14 |
| 9分 | x | 0.24 | |
| B | 8分 | 15 | 0.30 |
| 7分 | 8 | 0.16 | |
| C | 6分 | 4 | 0.08 |
| 5分 | 1 | y | |
| D | 5分以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?
