题目内容
3.梯形ABCD中,AD∥BC,AD=16,BC=20,AB=10,则CD的范围是6<CD<14.分析 作DE∥AB交BC于E,则四边形ABED是平行四边形,得出BE=AD=16,DE=AB=10,得出CE=BC-BE=4,在△CDE中,由三角形的三边关系定理即可得出结果.
解答 解:作DE∥AB交BC于E,如图所示:
则四边形ABED是平行四边形,
∴BE=AD=16,DE=AB=10,
∴CE=BC-BE=20-16=4,
在△CDE中,由三角形的三边关系定理得:10-4<CD<10+4,
即6<CD<14;
故答案为:6<CD<14.
点评 本题考查了梯形的性质、平行四边形的判定与性质、三角形的三边关系定理;熟练掌握梯形的性质,通过作辅助线得出平行四边形是解决问题的关键.

练习册系列答案
相关题目
13.已知$\frac{1}{x}-\frac{1}{y}=3$,则分式$\frac{2x+3xy-2y}{x-2xy-y}$的值为( )
| A. | $\frac{3}{5}$ | B. | 9 | C. | 1 | D. | 不能确定 |
18.下列各式中成立的是( )
| A. | x2y2=(x+y)(x-y) | B. | 1-x2=(1-x)2 | ||
| C. | (x2+4)(-4x)=(x-2)2 | D. | x2-$\frac{1}{4}x+\frac{1}{4}={(x-\frac{1}{2})^2}$ |
15.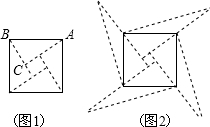 图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
 图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )| A. | 51 | B. | 49 | C. | 76 | D. | 无法确定 |
13.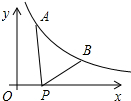 如图所示,已知A(1,y1),B(2,y2)为反比例函数y=$\frac{2}{x}$图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大值时,点P的坐标是( )
如图所示,已知A(1,y1),B(2,y2)为反比例函数y=$\frac{2}{x}$图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大值时,点P的坐标是( )
 如图所示,已知A(1,y1),B(2,y2)为反比例函数y=$\frac{2}{x}$图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大值时,点P的坐标是( )
如图所示,已知A(1,y1),B(2,y2)为反比例函数y=$\frac{2}{x}$图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大值时,点P的坐标是( )| A. | (3,0) | B. | ($\frac{7}{2}$,0) | C. | ($\frac{5}{3}$,0) | D. | ($\frac{5}{2}$,0) |