题目内容
2.(1)填空:(a-b)(a+b)=a2-b2,(a-b)(a2+ab+b2)=a3-b3,(a-b)(a3+a2b+ab2+b3)=a4-b4.
(2)猜想:(a-b)(an-1+an-2b+…+abn-2+bn-1)=an-bn(其中n为正整数,且n≥1);
(3)利用(2)猜想的结论计算:
29+28+27+…+23+22+2.
分析 (1)根据平方差公式与多项式乘以多项式的运算法则运算即可;
(2)根据(1)的规律可得结果;
(3)原式变形后,利用(2)得出的规律计算即可得到结果.
解答 解:(1)(a-b)(a+b)=a2-b2;
(a-b)(a2+ab+b2)=a3+a2b+ab2-a2b-ab2-b3=a3-b3;
(a-b)(a3+a2b+ab2+b3)=a4+a3b+a2b2+ab3-a3b-a2b2-ab3-b4=a4-b4;
(2)由(1)的规律可得:(a-b)(an-1+an-2b+…+abn-2+bn-1)=an-bn,
(3)29+28+27+…+23+22+2
=(2-1)•(29+28+27+…+23+22+2)
=210+29+28+27+…+23+22-(29+28+27+…+23+22+2)
=210-2
=1024-2
=1022.
故答案为:a2-b2,a3-b3,a4-b4;an-bn.
点评 此题考查了数字的变化规律和多项式乘以多项式,弄清题中的规律是解本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
10.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率分别稳定在0.15和0.45,则口袋中白色球的个数可能是( )
| A. | 28 | B. | 24 | C. | 16 | D. | 6 |
7.某农机厂四月份生产零件50万个,第二季度共生产临建182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是( )
| A. | 50+50(1+x)+50(1+x)2=182 | B. | 50(1+x)2=182 | ||
| C. | 50(1+2x)=182 | D. | 50+50(1+x)+50(1+2x)=182 |
 若关于x的不等式2x+a>-1的解集在数轴上表示如图,则a=3.
若关于x的不等式2x+a>-1的解集在数轴上表示如图,则a=3.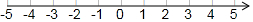
 一个进水管和与出水管的容器,从某时刻开始4分钟内只进水不出水,在随后的8分钟内既进水又出水,每分的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的函数关系如图所示.
一个进水管和与出水管的容器,从某时刻开始4分钟内只进水不出水,在随后的8分钟内既进水又出水,每分的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的函数关系如图所示.