题目内容
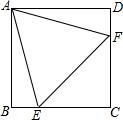已知如图，正方形ABCD中，等边△AEF的顶点E，F分别在边BC和CD上，求证：∠CEF=∠CFE．考点：全等三角形的判定与性质,正方形的性质
专题：证明题
分析：易证RT△ADF≌RT△ABE，根据全等三角形对应角相等的性质可得∠AFD=∠AEB，即可解题．
解答：证明：在正方形ABCD中，等边△AEF的顶点E、F分别在BC和CD上，
在RT△ADF和RT△ABE中，
，
∴RT△ADF≌RT△ABE（HL），
∴∠AFD=∠AEB，
∵∠AFE=∠AEF，
∴∠CEF=∠CFE．
在RT△ADF和RT△ABE中，
|
∴RT△ADF≌RT△ABE（HL），
∴∠AFD=∠AEB，
∵∠AFE=∠AEF，
∴∠CEF=∠CFE．
点评：本题考查了全等三角形的判定，考查了全等三角形对应角相等的性质，本题中求证RT△ADF≌RT△ABE是解题的关键．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
在山坡上种树，要求相邻两棵树之间的水平距离是3.5m，测得斜坡上相邻两树之间的坡面距离为5m，试求斜坡的倾斜角α的度数（精确到1°）如果点A（1，2）在直线y=3x+b上，则b的值为（ ）
| A、-1 | B、2 | C、3 | D、5 |
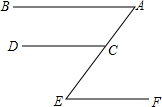如图，CD∥EF，∠ECD=∠A，则EF∥AB，说明理由如下：