题目内容
4.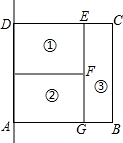 如图,某人用篱笆围成一个矩形菜园(墙壁足够长),他将矩形ABCD分为3个相等面积菜地为①、②、③,篱笆长为80m.设BC=x,ABCD面积为y,求y与x的解析式及x的取值范围,当x为多大时,y最大?
如图,某人用篱笆围成一个矩形菜园(墙壁足够长),他将矩形ABCD分为3个相等面积菜地为①、②、③,篱笆长为80m.设BC=x,ABCD面积为y,求y与x的解析式及x的取值范围,当x为多大时,y最大?
分析 根据三个矩形面积相等,得到矩形AEFD面积是矩形BCFE面积的2倍,可得出AE=2BE,设BE=a,则有AE=2a,表示出a与2a,进而表示出y与x的关系式,并求出x的范围即可;利用二次函数的性质求出y的最大值,以及此时x的值即可.
解答 解:∵三块矩形区域的面积相等,
∴矩形AEFD面积是矩形BCFE面积的2倍,
∴AE=2BE,
设BE=a,则AE=2a,
∴8a+2x=80,
∴a=-$\frac{1}{4}$x+10,2a=-$\frac{1}{2}$x+20,
∴y=(-$\frac{1}{2}$x+20)x+(-$\frac{1}{4}$x+10)x=-$\frac{3}{4}$x2+30x,
∵a=-$\frac{1}{4}$x+10>0,
∴x<40,
则y=-$\frac{3}{4}$x2+30x(0<x<40);
∵y=-$\frac{3}{4}$x2+30x=-$\frac{3}{4}$(x-20)2+300(0<x<40),且二次项系数为-$\frac{3}{4}$<0,
∴当x=20时,y有最大值,最大值为300平方米.
点评 此题考查了二次函数的应用,以及列代数式,熟练掌握二次函数的性质是解本题的关键.

练习册系列答案
相关题目
11. 若a、b在数轴上的位置如图所示,则下列各式中,一定正确的是( )
若a、b在数轴上的位置如图所示,则下列各式中,一定正确的是( )
 若a、b在数轴上的位置如图所示,则下列各式中,一定正确的是( )
若a、b在数轴上的位置如图所示,则下列各式中,一定正确的是( )| A. | -b<0 | B. | a、b互为相反数 | C. | a+b>a-b | D. | a-b>a |
 .
. 的平方根是( )
的平方根是( ) 的整数部分为m,小数部分为n,求
的整数部分为m,小数部分为n,求
 如图,已知四边形DEFG是△ABC的内接正方形,S△ADG=1,S△CFG=1,S△BDE=3,求△ABC的面积.
如图,已知四边形DEFG是△ABC的内接正方形,S△ADG=1,S△CFG=1,S△BDE=3,求△ABC的面积.