Question

20．在△ABC中，∠A=36°，AB=AC，BD是△ABC的角平分线，下列结论：
①△ABD，△BCD都是等腰三角形；
②AD=BD=BC；
③BC²=CD•CA；
④D是AC的黄金分割点
其中正确的是（　　）

• A． 1个
• B． 2个
• C． 3个
• D． 4个

Answer 1

分析 在△ABC，AB=AC，∠A=36°，BD平分∠ABC交AC于点D，可推出△BCD，△ABD为等腰三角形，可得AD=BD=BC，利用三角形相似解题．

解答 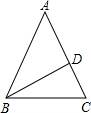解：如图，∵AB=AC，∠A=36°，
∴∠ABC=∠C=72°，
∵BD平分∠ABC交AC于点D，
∴∠ABD=∠CBD=$\frac{1}{2}$∠ABC=36°=∠A，
∴AD=BD，
∠BDC=∠ABD+∠A=72°=∠C，
∴BC=BD，
∴△ABD，△BCD都是等腰三角形，故①正确；
∴BC=BD=AD，故②正确；
∵∠A=∠CBD，∠C=∠C，
∴△BCD∽△ACB，
∴$\frac{BC}{AC}=\frac{CD}{BC}$，
即BC²=CD•AC，故③正确；
∵AD=BD=BC，
∴AD²=AC•CD=（AD+CD）•CD，
∴AD=$\frac{1+\sqrt{5}}{2}$CD，
∴D是AC的黄金分割点．故④正确，
故选D．

点评 本题考查了等腰三角形的判定与性质，相似三角形判定与性质．关键是明确图形中的三个等腰三角形的特点．