题目内容
11.已知抛物线y=mx2+2mx+m-2与x轴有两个不同的交点.(1)求m的取值范围;
(2)当此抛物线经过原点时,同时也经过点A(1,y1)、B(-2,y2),C(-3,y3)三点,试比较y1、y2与y3的大小.
分析 (1)先利用配方法将抛物线变形为顶点式,从而得到抛物线的顶点坐标为(-1,-2),当抛物线的开口向上时,抛物线与x轴由两个不同的交点;
(2)由抛物线经过原点可求得m=2,从而得到抛物线的解析式,然后可求得y1、y2、y3的值,然后再比较大小即可.
解答 解:(1)∵y=mx2+2mx+m-2=m(x2+2x+1)-2=m(x+1)2-2,
∴抛物线的顶点坐标为(-1,-2).
∴当m>0时,抛物线与x轴有两个不同的交点.
∴m的值范围是m>0.
(2)∵抛物线经过原点,
∴m-2=0.
解得:m=2.
∴抛物线的解析式为y=2(x+1)2-2.
将x=1时,y1=6;将x=-2时,y2=0;将x=-3时,y3=6.
∴y2<y1=y3.
点评 本题主要考查的是抛物线与x轴的交点,二次函数图象上点的坐标特征,求得m的值是解题的关键.

练习册系列答案
相关题目
2.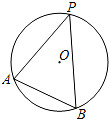 如图,⊙O是△ABP的外接圆,半径r=2,∠APB=45°,则弦AB的长为( )
如图,⊙O是△ABP的外接圆,半径r=2,∠APB=45°,则弦AB的长为( )
 如图,⊙O是△ABP的外接圆,半径r=2,∠APB=45°,则弦AB的长为( )
如图,⊙O是△ABP的外接圆,半径r=2,∠APB=45°,则弦AB的长为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |




 如图所示,把一根绳子对折成线段AB,从P处把绳子剪断,已知AP=$\frac{1}{3}$PB,若剪断后的各段绳子中最长的一段为60cm,则绳子的原长为200cm.
如图所示,把一根绳子对折成线段AB,从P处把绳子剪断,已知AP=$\frac{1}{3}$PB,若剪断后的各段绳子中最长的一段为60cm,则绳子的原长为200cm.