题目内容
10. 我们知道,面积为2的正方形的边长a是一个无理数,即a是一个无限不循环小数,根据这个基本事实,回答下列问题.
我们知道,面积为2的正方形的边长a是一个无理数,即a是一个无限不循环小数,根据这个基本事实,回答下列问题.(1)若m、n是最接近a的两个正整数,则m+n等于3;
(2)a2-2015等于-2013;
(3)用圆规和三角板,在下列数周上画出表示a和-a的两个点.(保留画图痕迹)
分析 (1)根据正方形的面积求出边长,求出$\sqrt{2}$的范围,即可得出答案;
(2)把a=$\sqrt{2}$代入求出即可;
(2)作边长为1的正方形ABCD,连接AC,以A为圆心,以AC为半径作弧,交数轴于两点.
解答 解:(1)面积为2的正方形的边长a=$\sqrt{2}$,
∵1$<\sqrt{2}$<2,
∴m=1,n=2,
∴m+n=3,
故答案为:3;
(2)a2-2015=($\sqrt{2}$)2-2015=-2013,
故答案为:-2013;
(3)如图所示,正方形ABCD的边长为1个单位长度 .
.
点评 本题考查了数轴,估算无理数的大小的应用,能求出$\sqrt{2}$的范围是解此题的关键.

练习册系列答案
相关题目
2.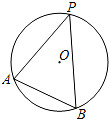 如图,⊙O是△ABP的外接圆,半径r=2,∠APB=45°,则弦AB的长为( )
如图,⊙O是△ABP的外接圆,半径r=2,∠APB=45°,则弦AB的长为( )
 如图,⊙O是△ABP的外接圆,半径r=2,∠APB=45°,则弦AB的长为( )
如图,⊙O是△ABP的外接圆,半径r=2,∠APB=45°,则弦AB的长为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |