题目内容
3.已知二次函数y=2x2+5x-3的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C.试写出A,B,C三点的坐标.分析 把y=0代入y=2x2+5x-3得出2x2+5x-3=0,求出方程的解,即可得出A、B的坐标,把x=0代入y=2x2+5x-3即可求出C的坐标.
解答 解:令y=2x2+5x-3=0,
即2x2+5x-3=0,
解得x1=-3,x2=$\frac{1}{2}$,
所以A(-3,0),B($\frac{1}{2}$,0),
令x=0,y=-3,
则C(0,-3),
综上A(-3,0),B($\frac{1}{2}$,0),C(0,-3).
点评 本题主要考查了抛物线与x轴的交点坐标的知识,解答本题的关键是根据题意列出一元二次方程求交点坐标,此题难度一般.

练习册系列答案
相关题目
13.下列计算正确的是( )
| A. | 5ab-3ab=2 | B. | (1+$\sqrt{2}$)(1-$\sqrt{2}$)=1 | C. | -(-a)4÷a2=a2 | D. | (xy)-2=$\frac{1}{{x}^{2}{y}^{2}}$ |
14.甲、乙两人每次都从五个数-2,-1,0,1,2中任取一个,分别记作(x,y),则这些坐标表示的点在直线y=x+1上的概率为( )
| A. | $\frac{4}{25}$ | B. | $\frac{8}{25}$ | C. | $\frac{9}{25}$ | D. | $\frac{2}{5}$ |
15.下列计算正确的是( )
| A. | -x2+3x2=2 | B. | x2×x3=x6 | ||
| C. | (x+1)(-x-1)=-x2-2x-1 | D. | $\frac{{x}^{2}-4}{x-2}$=x-2 |
12.已知y=-x(x+3-a)+1是关于x的二次函数,当x的取值范围在1≤x≤5时,y在x=1时取得最大值,则实数a的取值范围是( )
| A. | a=9 | B. | a=5 | C. | a≤9 | D. | a≤5 |
13.方程x2-2x=3可以化简为( )
| A. | (x-3)(x+1)=0 | B. | (x+3)(x-1)=0 | C. | (x-1)2=2 | D. | (x-1)2+4=0 |
 将如图方格纸中的线段AB平移,分别画出经下列平移后所得的图形:
将如图方格纸中的线段AB平移,分别画出经下列平移后所得的图形: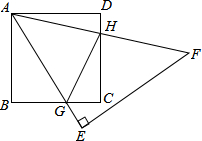 如图,已知正方形ABCD和等腰直角三角形△AEF,∠E=90°,AE和BC交于点G,AF和CD交于点H,正方形ABCD的面积为1cm2,则△CGH的周长为2.
如图,已知正方形ABCD和等腰直角三角形△AEF,∠E=90°,AE和BC交于点G,AF和CD交于点H,正方形ABCD的面积为1cm2,则△CGH的周长为2.