题目内容
9. 如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G,下列结论正确的有( )个.
如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G,下列结论正确的有( )个.①BF=AC;②AE=$\frac{1}{2}$BF;③∠A=67.5°;④△DGF是等腰三角形;⑤S四边形ADGE=S四边形GHCE.
| A. | 5个 | B. | 2个 | C. | 4个 | D. | 3个 |
分析 只要证明△BDF≌△CDA,△BAC是等腰三角形,∠DGF=∠DFG=67.5°,即可判断①②③④正确,作GM⊥BD于M,只要证明GH<DG即可判断⑤错误.
解答 解:∵CD⊥AB,BE⊥AC,
∴∠BDC=∠ADC=∠AEB=90°,
∴∠A+∠ABE=90°,∠ABE+∠DFB=90°,
∴∠A=∠DFB,
∵∠ABC=45°,∠BDC=90°,
∴∠DCB=90°-45°=45°=∠DBC,
∴BD=DC,
在△BDF和△CDA中
$\left\{\begin{array}{l}{∠BDF=∠CDA}\\{∠A=∠DFB}\\{BD=CD}\end{array}\right.$,
∴△BDF≌△CDA(AAS),
∴BF=AC,故①正确.
∵∠ABE=∠EBC=22.5°,BE⊥AC,
∴∠A=∠BCA=67.5°,故③正确,
∴BA=BC,
∵BE⊥AC,
∴AE=EC=$\frac{1}{2}$AC=$\frac{1}{2}$BF,故②正确,
∵BE平分∠ABC,∠ABC=45°,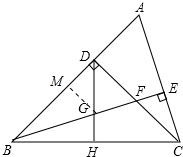
∴∠ABE=∠CBE=22.5°,
∵∠BDF=∠BHG=90°,
∴∠BGH=∠BFD=67.5°,
∴∠DGF=∠DFG=67.5°,
∴DG=DF,故④正确.
作GM⊥AB于M.
∵∠GBM=∠GBH,GH⊥BC,
∴GH=GM<DG,
∴S△DGB>S△GHB,
∵S△ABE=S△BCE,
∴S四边形ADGE<S四边形GHCE.故⑤错误,
∴①②③④正确,
故选C.
点评 此题是三角形综合题,考查了等腰三角形的性质,直角三角形的性质,全等三角形的性质和判定,三角形的面积等知识点的综合运用,第五个问题难度比较大,添加辅助线是解题关键,属于中考选择题中的压轴题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.下列各式的因式分解结果中,正确的是( )
| A. | 6x2-8x=x(6x-8) | B. | a2+4b2-4ab=(a-2b)2 | ||
| C. | 8xyz-6x2y2=2xyz(4-3xy) | D. | 4a2-b2=(4a-b)(4a+b) |
10.某学校在八年级开设了数学史、诗词赏析、陶艺三门校本课程,若小波和小睿两名同学每人随机选择其中一门课程,则小波和小睿选到同一课程的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{9}$ |

 从A地到B地需修一条公路,该工程由甲、乙两队共同完成,甲、乙两队分别从A地、B地同时开始修路,设修路的时间为x(天),未修的路程为y(米),图中的折线表示甲乙两个工程队从开始施工到工程结束的过程中y与x之间的函数关系.已知在修路过程中,甲工程队因设备升级而停工5天,则设备升级后甲工程队每天修路比原来多533$\frac{1}{3}$米.
从A地到B地需修一条公路,该工程由甲、乙两队共同完成,甲、乙两队分别从A地、B地同时开始修路,设修路的时间为x(天),未修的路程为y(米),图中的折线表示甲乙两个工程队从开始施工到工程结束的过程中y与x之间的函数关系.已知在修路过程中,甲工程队因设备升级而停工5天,则设备升级后甲工程队每天修路比原来多533$\frac{1}{3}$米.