Question

2．如图，在平面直角坐标系中有一菱形OABC且∠A=120°，点O、B在y轴上，OA=1，现在把菱形向右无滑动翻转，每次翻转60°，点B的落点依次为B₁、B₂、B₃…，连续翻转2017次，则B₂₀₁₇的坐标为（1345.5，$\frac{\sqrt{3}}{2}$）．

Answer 1

分析 连接AC，根据条件可以求出AC，画出第5次、第6次、第7次翻转后的图形，容易发现规律：每翻转6次，图形向右平移4．由于2017=336×6+1，因此点B₁向右平移1344（即336×4）即可到达点B₂₀₁₇，根据点B₅的坐标就可求出点B₂₀₁₇的坐标．

解答 解：连接AC，如图所示．
∵四边形OABC是菱形，
∴OA=AB=BC=OC．
∵∠ABC=60°，
∴△ABC是等边三角形．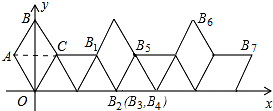
∴AC=AB．
∴AC=OA．
∵OA=1，
∴AC=1．
画出第5次、第6次、第7次翻转后的图形，如图所示．
由图可知：每翻转6次，图形向右平移4个单位．
∵2017=336×6+1，
∴点B₁向右平移1344（即336×4）到点B₂₀₁₇．
∵B₁的坐标为（1.5，$\frac{\sqrt{3}}{2}$），
∴B₂₀₁₇的坐标为（1.5+1344，$\frac{\sqrt{3}}{2}$），
∴B₂₀₁₇的坐标为（1345.5，$\frac{\sqrt{3}}{2}$）．
故答案为（1345.5，$\frac{\sqrt{3}}{2}$）

点评 本题考查了菱形的性质、等边三角形的判定与性质等知识，考查了操作、探究、发现规律的能力．发现“每翻转6次，图形向右平移4个单位”是解决本题的关键．