题目内容
18.当x满足x>$\frac{3}{5}$时,分式$\frac{3-5x}{3+(x-1)^{2}}$的值为负.分析 分式的分子为负数,分母为正数,根据异号两数相除商为负,得到分式的分子为负数,即可得到结论.
解答 解:∵分式$\frac{3-5x}{3+(x-1)^{2}}$的值为负,
∴3-5x<0,
∴x>$\frac{3}{5}$,
故答案为:$\frac{3}{5}$.
点评 本题考查了分式的值,解不等式,正确的理解题意是解题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
10.已知下列各式:①$\frac{1}{x}$+y=2,②2x-3y=5,③x+xy=2,④x+y=z-1,⑤$\frac{x+1}{2}$=$\frac{2x-1}{3}$,其中二元一次方程的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.下列各式是一元一次方程的是( )
| A. | x+3y=4 | B. | x2-2x=6 | C. | -6x=0 | D. | x-1═$\frac{1}{x}$ |
8.某公司今年4月分营业额为60万元,6月份营业额达到100万元,设该公司5,6两个月营业额的月平均增长率为x,则下列方程中正确的是( )
| A. | 60(1+2x)=100 | B. | 100(1+x)2=60 | ||
| C. | 60(1+x)2=100 | D. | 60+60(1+x)+60(1+x)2=100 |
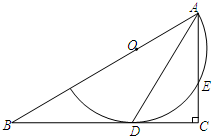 如图,△ABC中,∠C=90°,点O为AB上的一点,以点O为圆心,OA为半径的圆弧与BC相切于点D,交AC于点E,连接AD.
如图,△ABC中,∠C=90°,点O为AB上的一点,以点O为圆心,OA为半径的圆弧与BC相切于点D,交AC于点E,连接AD.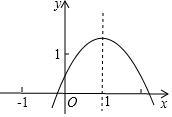 已知二次函数y=ax2+bx+c(a≠0)的对称轴是直线x=1,图象如图所示.给出下面五个结论:①abc>0;②2a+b=0;③b2-4ac>0;④a+b>m(am+b)(m为实数,且m≠1);⑤2c>3b.
已知二次函数y=ax2+bx+c(a≠0)的对称轴是直线x=1,图象如图所示.给出下面五个结论:①abc>0;②2a+b=0;③b2-4ac>0;④a+b>m(am+b)(m为实数,且m≠1);⑤2c>3b.